Pada halaman ini akan dibahas mengenai Soal Gaya Pegas dan Pembahasan. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Soal 1
Sebuah pegas membutuhkan gaya 4,5 N untuk memampatkannya dari panjang 40 cm menjadi 35 cm. Hitung konstanta pegas, k.
Jawab:
Kita bisa menulis hukum Hooke dalam hal nilai absolut:
|F| = k|Δx|
Sekarang |Δx| = 5 cm, jadi kita punya
4,5 N = k (5 cm)
k = 0,9 N/cm = 90 N/m
Soal 2
Massa M dilekatkan pada dua pegas seperti yang ditunjukkan pada gambar. Pegas di sebelah atas dikompres 20 cm dari panjang aslinya. Hitung gaya yang dibutuhkan untuk menggerakkan massa 10 cm ke atas, dengan kecepatan konstan.
Jawab:
Dalam situasi ini, pegas di sebelah kiri perlu dikompres, dan karena pegas di sebelah kanan dikompres, akan memberikan beberapa gaya yang dibutuhkan untuk menggerakkan massa. Kita tidak mempercepat misa, jadi kita tidak harus mengerahkan kekuatan bersih hanya untuk memindahkannya.Gaya yang dibutuhkan untuk memampatkan pegas di sebelah atas adalahF1 = - (k1 ∆x1) = - (120 N/m) (- 0,01 m) = 1,2 N Gaya ke atas yang dihasilkan oleh pegas di sebelah bawah adalahF2 = - (k2∆x2) = -(80 N/m)(0,01 m) = -0,8 N Sekarang gaya bersih yang dibutuhkan untuk melakukan perpindahan adalah jumlah kedua kekuatan ini,F1 + F2 = 1,2 N - 0,8 N = 0,4 N.
Soal 3
Dua pegas, dengan konstanta pegas k1 = 200 N/m dan k2 = 100 N/m dilekatkan seperti ditunjukkan pada gambar. Hitung jumlah gaya yang dibutuhkan untuk memampatkan pegas sebesar 10 cm.
Jawab:
konstanta pegas gabungan adalah1/kt = 1/k1 + 1/k21/kt = 1/(200 N/m) + 1/(100 N/m)kt = 66,67 N/m Sekarang untuk menemukan gaya kita hanya menggunakan hukum Hooke:F = -kx = - (66,67 N/m) (-0,010 mF = 0,667 N
Soal 4
Dua pegas dilekatkan pada balok seperti yang ditunjukkan pada gambar. Hitung gaya yang dibutuhkan untuk kompres keduanya sebesar 10 cm.
Jawab:
Dalam kasus ini, konstanta pegas keseluruhan k hanyalah jumlah konstanta masing-masing pegas:k = k1 + k2 Jadi k = 120 N/m + 80 N/m = 200 N/m. Sekarang ini adalah perhitungan langsung dari gaya menggunakan hukum Hooke dan perpindahannya, |Δx| = 10 cmF = k|Δx| = (200 N/m)(0,01 m) = 2 N Gaya yang dibutuhkan untuk memampatkan atau memperpanjang beberapa pegas hanyalah jumlah gaya untuk memampatkan/memperpanjang setiap pegas secara terpisah. Dalam hal ini, pegas dikatakan bekerja secara paralel.
Soal 5
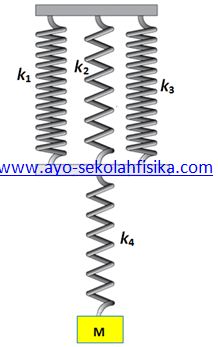Siatem pegas gabungan di bawah ini disusun atas empat pegas dengan k1 = 80 N/M, k2 = 120 N/m, k3 = 80 N/m dan k4 = 120 N/m, jika sistem tersebut diberi beban dengan massa 200 kg, tentukan (a) konstanta pegas total sistem (b) gaya yang dialami oleh masing-masing pegas dan pertambahan panjang masing-masing pegas!
Jawab:
(a) Dari sistem tersebut k1, k2 dan k3 disusun paralel maka,
kp = k1 + k2 + k3 = 80 N/m + 120 N/m + 80 N/m = 280 N/m
sedangkan kp seri dengan k4 maka
ktotal = kpk4/(kp + k4) = (280 N/m)(120 N/m)/(280 N/m + 120 N/m) = 84 N/m
(a) gaya total sistem adalah F = mg = 2000 N,
untuk sistem pegas yang disusun seri gaya tarik untuk masing-masing pegas sama besar maka,
F4 = FP = F = 2000 N
maka ∆x4 = F/k4 = 2000 N/(120 N/m) = 50/3 cm
sedangkan jumlah gaya untuk ketiga pegas k1,k2 dan k3 yang disusun paralel harus sama dengan F4 = 2000 N sedangkan pertambahan panjang pegas untuk masing-masing pegas k1,k2 dan k3 adalah sama besar yaitu ∆x = FP/kp = (2000 N)/(280 N/m) = 50/7 meter = ∆x1 = ∆x2 = ∆x3, sehingga besar gaya untuk masing-masing pegas k1,k2 dan k3 adalah
F1 = k1∆x = (80 N/m)(50/7 m) = 4000/7 N = 571,43 N
F2 = k2∆x = (120 N/m)(50/7 m) = 6000/7 N = 857,14 N
F1 = k1∆x = (80 N/m)(50/7 m) = 571,43 N
Soal 6
Perhatikan dua sistem susunan pegas di bawah ini!. Tentukan perbandingan pertambahan panjang sistem yang bermassa M dan sistem yang bermassa 3M jika k1 = k3 = k5 = 2k dan k2 = k4 = k!
Jawab:
Untuk sistem pegas yang memiliki massa M, susunan pegas paralelnya adalah
kp = k1 + k2 + k3 = 2k + k + 2k = 5k
maka konstanta pegas totalnya adalah
1/kT = 1/kp + 1/k4 atau kT = kpk4/(kp + k4) = (5k)(k)/(5k + k) = 5k/6
karena pertambahan panjang pegas ∆x = F/k, maka ∆xM = 6Mg/5k
Untuk sistem pegas yang memiliki massa 3M, susunan pegas paralelnya adalah
kp1 = k1 + k2 + k3 = 2k + k + 2k = 5k
kp2 = k4 + k5 = k + 2k = 3k
maka konstanta pegas totalnya adalah
1/kT = 1/kp1 + 1/kp2 atau kT = kp1kp2/(kp1 + kp2) = (5k)(3k)/(5k + 3k) = 15k/8
karena pertambahan panjang pegas ∆x3M = F/k, maka ∆x3M = 24Mg/15k
sehingga,
Soal 7
Sebuah pegas digantung pada langit-langit sebuah lift. Pada bawah pegas diberi beban 50 gram. Bila lift diam pegas bertambah panjang 10 cm. Tentukan pertambahan panjang pegas ketika lift sedang bergerak: (a) ke atas dengan percepatan 4 m/s2 dan (b) ke bawah dengan percepatan 4 m/s2. Ambil g = 10 m/s2!
Jawab:
Massa beban m = 50 gram = 50 x 10-3 kg dan percepatan gravitasi g = 10 m/s2.
Ketika lift diam (a = 0) pegas bertambah panjang x = 10 cm = 0,1 m. Menurut hukum II Newton:
ΣF = ma
kx – mg = 0
kx = mg
k = mg/x = (50 x 10-3 kg)(10 m/s2)/0,1 m = 5 N/m
(a) Pertambahan panjang x ketika lift bergerak ke atas dengan percepatan a = +4 m/s2 (ke atas)
ΣF = ma
+kx – mg = ma
kx = m(g + a)
x = m(g + a)/k
= (50 x 10-3 kg)(10 m/s2 + 4 m/s2)/5 N/m
x = 0,14 m = 14 cm
(b) Pertambahan panjang x ketika lift bergerak ke bawah dengan percepatan a = -4 m/s2 (ke bawah)
ΣF = ma
–kx + mg = ma
kx = m(g – a)
x = m(g – a)/k
= (50 x 10-3 kg)(10 m/s2 – 4 m/s2)/5 N/m
x = 0,06 m = 6 cm
Sebuah pegas membutuhkan gaya 4,5 N untuk memampatkannya dari panjang 40 cm menjadi 35 cm. Hitung konstanta pegas, k.
Jawab:
Kita bisa menulis hukum Hooke dalam hal nilai absolut:
|F| = k|Δx|
Sekarang |Δx| = 5 cm, jadi kita punya
4,5 N = k (5 cm)
k = 0,9 N/cm = 90 N/m
Soal 2
Massa M dilekatkan pada dua pegas seperti yang ditunjukkan pada gambar. Pegas di sebelah atas dikompres 20 cm dari panjang aslinya. Hitung gaya yang dibutuhkan untuk menggerakkan massa 10 cm ke atas, dengan kecepatan konstan.Jawab:
Dalam situasi ini, pegas di sebelah kiri perlu dikompres, dan karena pegas di sebelah kanan dikompres, akan memberikan beberapa gaya yang dibutuhkan untuk menggerakkan massa. Kita tidak mempercepat misa, jadi kita tidak harus mengerahkan kekuatan bersih hanya untuk memindahkannya.Gaya yang dibutuhkan untuk memampatkan pegas di sebelah atas adalahF1 = - (k1 ∆x1) = - (120 N/m) (- 0,01 m) = 1,2 N Gaya ke atas yang dihasilkan oleh pegas di sebelah bawah adalahF2 = - (k2∆x2) = -(80 N/m)(0,01 m) = -0,8 N Sekarang gaya bersih yang dibutuhkan untuk melakukan perpindahan adalah jumlah kedua kekuatan ini,F1 + F2 = 1,2 N - 0,8 N = 0,4 N.
Soal 3
Dua pegas, dengan konstanta pegas k1 = 200 N/m dan k2 = 100 N/m dilekatkan seperti ditunjukkan pada gambar. Hitung jumlah gaya yang dibutuhkan untuk memampatkan pegas sebesar 10 cm.
konstanta pegas gabungan adalah1/kt = 1/k1 + 1/k21/kt = 1/(200 N/m) + 1/(100 N/m)kt = 66,67 N/m Sekarang untuk menemukan gaya kita hanya menggunakan hukum Hooke:F = -kx = - (66,67 N/m) (-0,010 mF = 0,667 N
Soal 4
Dua pegas dilekatkan pada balok seperti yang ditunjukkan pada gambar. Hitung gaya yang dibutuhkan untuk kompres keduanya sebesar 10 cm.
Dalam kasus ini, konstanta pegas keseluruhan k hanyalah jumlah konstanta masing-masing pegas:k = k1 + k2 Jadi k = 120 N/m + 80 N/m = 200 N/m. Sekarang ini adalah perhitungan langsung dari gaya menggunakan hukum Hooke dan perpindahannya, |Δx| = 10 cmF = k|Δx| = (200 N/m)(0,01 m) = 2 N Gaya yang dibutuhkan untuk memampatkan atau memperpanjang beberapa pegas hanyalah jumlah gaya untuk memampatkan/memperpanjang setiap pegas secara terpisah. Dalam hal ini, pegas dikatakan bekerja secara paralel.
Soal 5
Siatem pegas gabungan di bawah ini disusun atas empat pegas dengan k1 = 80 N/M, k2 = 120 N/m, k3 = 80 N/m dan k4 = 120 N/m, jika sistem tersebut diberi beban dengan massa 200 kg, tentukan (a) konstanta pegas total sistem (b) gaya yang dialami oleh masing-masing pegas dan pertambahan panjang masing-masing pegas!Jawab:
(a) Dari sistem tersebut k1, k2 dan k3 disusun paralel maka,
kp = k1 + k2 + k3 = 80 N/m + 120 N/m + 80 N/m = 280 N/m
sedangkan kp seri dengan k4 maka
ktotal = kpk4/(kp + k4) = (280 N/m)(120 N/m)/(280 N/m + 120 N/m) = 84 N/m
(a) gaya total sistem adalah F = mg = 2000 N,
untuk sistem pegas yang disusun seri gaya tarik untuk masing-masing pegas sama besar maka,
F4 = FP = F = 2000 N
maka ∆x4 = F/k4 = 2000 N/(120 N/m) = 50/3 cm
sedangkan jumlah gaya untuk ketiga pegas k1,k2 dan k3 yang disusun paralel harus sama dengan F4 = 2000 N sedangkan pertambahan panjang pegas untuk masing-masing pegas k1,k2 dan k3 adalah sama besar yaitu ∆x = FP/kp = (2000 N)/(280 N/m) = 50/7 meter = ∆x1 = ∆x2 = ∆x3, sehingga besar gaya untuk masing-masing pegas k1,k2 dan k3 adalah
F1 = k1∆x = (80 N/m)(50/7 m) = 4000/7 N = 571,43 N
F2 = k2∆x = (120 N/m)(50/7 m) = 6000/7 N = 857,14 N
F1 = k1∆x = (80 N/m)(50/7 m) = 571,43 N
Soal 6
Perhatikan dua sistem susunan pegas di bawah ini!. Tentukan perbandingan pertambahan panjang sistem yang bermassa M dan sistem yang bermassa 3M jika k1 = k3 = k5 = 2k dan k2 = k4 = k!
Untuk sistem pegas yang memiliki massa M, susunan pegas paralelnya adalah
kp = k1 + k2 + k3 = 2k + k + 2k = 5k
maka konstanta pegas totalnya adalah
1/kT = 1/kp + 1/k4 atau kT = kpk4/(kp + k4) = (5k)(k)/(5k + k) = 5k/6
karena pertambahan panjang pegas ∆x = F/k, maka ∆xM = 6Mg/5k
Untuk sistem pegas yang memiliki massa 3M, susunan pegas paralelnya adalah
kp1 = k1 + k2 + k3 = 2k + k + 2k = 5k
kp2 = k4 + k5 = k + 2k = 3k
maka konstanta pegas totalnya adalah
1/kT = 1/kp1 + 1/kp2 atau kT = kp1kp2/(kp1 + kp2) = (5k)(3k)/(5k + 3k) = 15k/8
karena pertambahan panjang pegas ∆x3M = F/k, maka ∆x3M = 24Mg/15k
sehingga,
Sebuah pegas digantung pada langit-langit sebuah lift. Pada bawah pegas diberi beban 50 gram. Bila lift diam pegas bertambah panjang 10 cm. Tentukan pertambahan panjang pegas ketika lift sedang bergerak: (a) ke atas dengan percepatan 4 m/s2 dan (b) ke bawah dengan percepatan 4 m/s2. Ambil g = 10 m/s2!
Jawab:
Massa beban m = 50 gram = 50 x 10-3 kg dan percepatan gravitasi g = 10 m/s2.
Ketika lift diam (a = 0) pegas bertambah panjang x = 10 cm = 0,1 m. Menurut hukum II Newton:
ΣF = ma
kx – mg = 0
kx = mg
k = mg/x = (50 x 10-3 kg)(10 m/s2)/0,1 m = 5 N/m
(a) Pertambahan panjang x ketika lift bergerak ke atas dengan percepatan a = +4 m/s2 (ke atas)
ΣF = ma
+kx – mg = ma
kx = m(g + a)
x = m(g + a)/k
= (50 x 10-3 kg)(10 m/s2 + 4 m/s2)/5 N/m
x = 0,14 m = 14 cm
(b) Pertambahan panjang x ketika lift bergerak ke bawah dengan percepatan a = -4 m/s2 (ke bawah)
ΣF = ma
–kx + mg = ma
kx = m(g – a)
x = m(g – a)/k
= (50 x 10-3 kg)(10 m/s2 – 4 m/s2)/5 N/m
x = 0,06 m = 6 cm
Tidak ada komentar:
Posting Komentar