Pada halaman ini akan dibahas mengenai Hukum Biot-Savart (Medan Magnetik). Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Seperti halnya untuk medan listrik, ada sebuah prinsip superposisi medan-medan magnetik (principle of superposition of magnetic fields); medan magnet total yang disebabkan oleh beberapa muatan yang bergerak adalah jumlah vektor dari medan-medan yang disebabkan oleh masing-masing muatan. Kita menggunakan prinsip ini untuk mencari medan magnet yang dihasilkan oleh sebuah arus listrik yang mengalir dalam suatu penghantar (konduktor).
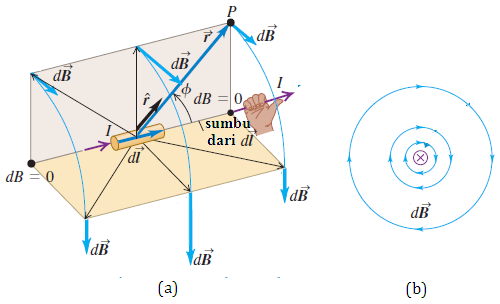
Kita mulai dengan menghitung medan magnet yang disebabkan oleh sebuah elemen pendek dldari sebuah konduktor pengangkut arus, seperti yang diperlihatkan pada gambar 1. Volume segmen itu adalah A dl, dengan A adalah luas penampang konduktor tiu. Jika terdapat n partikel bermuatan q, maka muatan total yang bergerak dQ dalam segmen itu adalah
dQ = nqA dl
Muatan yang bergerak dalam segmen ini ekivalen dengan sebuah muatan tunggal dQ yang bergerak dengan kecepatan yang sama dengan kecepatan penyimpang (drift), vd. Medan magnet yang ditimbulkan dari gerakan acak dari muatan itu secara rata-rata akan saling meniadakan di setiap titik. Maka besarnya medan magnet dB yang dihasilkan disebarang titik medan P adalah
karena nIqIvdA sama dengan arus I dalam elemen itu, maka sumbu dari
dalam bentuk vektor, dengan menggunakan vektor kita tuliskan persamaan (1) sebagai
medan magnetik sebuah elemen arus.
dengan dladalah sebuah vektor dengan panjang dl, dengan arah yang sama dengan arus dalam konduktor.
Persamaan (1) dan (2) dinamakan hukum Biot dan Savart. Kita dapat menggunakan hukum ini untuk mencari medan magnetik total Bdi sebarang titik dalam ruang yang ditimbulkan oleh arus dalam suatu rangkaian lengkap. Untuk melakukan ini, kita mengintegralkan persamaan (2) terhadap semua elemen dl yang mengangkut arus, maka
Kita tidak dapat membuktikan secara langsung persamaan (1) dan (2) karena kita tidak perna dapat berekperimen dengan sebuah segmen yang terisolasi dari sebuah rangkaian pengangkut arus. Apa yang kita ukur secara ekperimental adala Btotal untuk suatu rangkaian lengkap. Tetapi kita masih dapat membuktikan persamaan-persamaan ini secara tidak langsung dengan menghitung B untuk berbagai konfigurasi arus dengan menggunakan persamaan (3) dan dengan membandingkan hasil-hasil itu dengan pengukuran ekperimen.




Tidak ada komentar:
Posting Komentar