Pada halaman ini akan dibahas mengenai Kecepatan & Percepatan Gerak Harmonik Sederhana. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
 |
| Gambar 1: Grafik yang menunjukkan (a) Pepindahan GHS, (b) kecepatan GHS dan (c) Percepatan GHS |
Gambar 1a, menunjukkan grafik perpindahan terhadap waktu yang diberikan oleh persamaan x = A cos (ωt + φ). Kita dapat menemukan kecepata v sebagai fungsi waktu dari grafik 2, besar dari v adalah vmaks sin Ө, tetapi v mengarah ke kiri, sehingga v = - vmaks sin Ө. Lagi lagi dengan mengatur Ө = ωt = 2∏ft = 2∏t/T kita dapatkan
Hanya setelah t = 0, kecepatan negatif (mengarah ke kiri) dan tetap begitu sampai t = ½ T (sesuai dengan Ө = 1800 = ∏ radian). Setelah t= ½ T sampai t= T kecepatannya positif. Kecepatan sebagai fungsi waktu di atas diplot di gambar 1b. Karena frekuensi gerak harmonik sederhana adalah f = 1/2∏ (k/m)1/2, maka
untuk sebuah sistem pegas massa tersebut, laju maksimum vmaks lebih besar ketika amplitudonya lebih besar, dan selalu terjadi saat massanya melewati titik setimbang.
 |
| Gambar 2 |
Hukum II Newton memberi kita percepatan sebagai fungsi waktu:
di mana percepatan maksimumnya adalah
Persamaan percepatan sebagai fungsi waktu ini diplot pada gambar 1c. Karena percepatan GHS tidak konstan, persamaan untuk gerak dipercepat beraturan tidak berlaku untuk GHS.
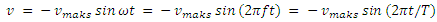



Tidak ada komentar:
Posting Komentar