Pada halaman ini akan dibahas mengenai Soal dan Penyelesaian GLB dan GLBB. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Soal 1
Sebuah mobil bergerak lurus beraturan dan menempuh 3 km dalam waktu 2 menit. Berapa lama diperlukan mobil itu untuk menempuh 75 km?
Solusi:
Diketahui: x0 = 0; v = 3/2 km/menit dan x = 75 km.
pada gerak lurus dengan kecepatan tetap, berlaku
x = x0 + vt
75 km = 0 + (1,5 km/menit)t
t = 50 menit
Soal 2
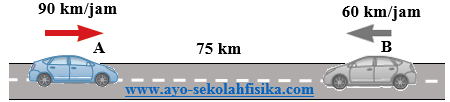
Dua buah mobil yang terpisah sejauh 75 km bergerak saling mendekat, pada saat bersamaan, masing-masing dengan kecepatan 90 km/jam dan 60 km/jam. Kapan dan di mana kedua mobil tersebut berpapasan?
Solusi:
Cara I:
Jika kita ambil titik acuan di mobil A, maka: x0A = 0, vA = 90 km/jam; tA = tB = T (waktu bersamaan); vB = - 60 km/jam (minus karena ke kiri), x0B = 75 km.
Kedua mobil berpapasan jika posisi mobil A sama dengan posisi mobil B, yaitu:
xA = xB
x0A + vAtA = x0B + v0BtB
0 + (90 km/jam)T = 75 km + (- 60 km/jam)T
T = 0,5 jam (waktu kedua mobil berpapasan)
Posisi berpapasan dapat diperoleh dari
xA = x0A + vAtA = 0 + (90 km/jam)(0,5 jam) = 45 km dari mobil A mula-mula.
Cara II:
Sebuah mobil bergerak dengan kecepatan 27 km/jam, kemudian mobil ini dipercepat dengan percepatan 2 m/s2. Hitung kecepatan dan jarak yang ditempuh selama 5 detik setelah pemercepat itu.
Solusi:
Diketahui: v0 = 27 km/jam = 7,5 m/s; a = 2 m/s2; t = 5 s dan dan x0 = 0.
Dengan menggunakan,
v = v0 + at = 7,5 m/s + (2 m/s2)(5 s) = 17,5 m/s
dan x = x0 + v0t + ½ at2 = 0 + (7,5 m/s)(5 s) + ½ (2 m/s2)(5 s)2 = 62,5 m
Soal 4
Sebuah sepeda motor bergerak dengan kecepatan 54 km/jam. Tiba-tiba motor tersebut direm mendadak dan berhenti setelah 2 detik. Hitung jarak yang ditempuh motor tersebut selama pengereman.
Solusi:
v0 = 54 km/jam = 15 m/s; t = 2 s; x0 = 0; v = 0 (berhenti). Kita gunakan, x = 1/2 (v0 + v)t = 1/2 (15 m/s + 0) . 2 s = 15 m
Soal 5
Sebuah kereta api awalnya bergerak dengan kecepatan tetap 90 km/jam. Tiba-tiba kereta direm mendadak dengan perlambatan 8 m/s2. Setelah berapa detik kereta itu menempuh jarak 21 meter dari saat kereta tersebut direm.
Solusi
Diketahui: a = - 8 m/s2; x0 = 0; v0 = 90 km/jam = 25 m/s; x = 21 m, maka dengan
x = x0 + v0t + ½ at2
21 m = 0 + (25 m/s)t + ½ (-8 m/s2)t2
0 = 4t2 – 25t + 21
Atau 0 = (4t – 21)(t – 1)
t1 = 21/4 = 5,25 sekon; t2 = +1 sekon
kita disini mendapatkan dua hasil yang berbeda, hal ini bisa dijelaskan sebagai berikut: anggap P berjarak 21 m dari posisi kereta ketika direm. Pertama kali kereta melewati A dalam waktu 1 s namun karena kereta terus diperlambat, maka kecepatan kereta akhirnya negatif, kereta bergerak mundur dan akan kembali ke titik P setelah 5,25 sekon.
Soal 6
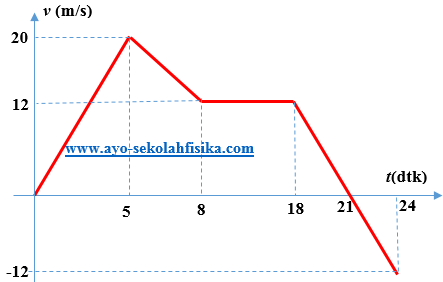
Gambar (2) di bawah ini merupakan grafik kecepatan versus waktu dari sebuah mobil yang bergerak sepanjang jalan lurus.
Tentukan: (a) jarak total yang ditempuh mobil tersebut, (b) perpindahan total yang ditempuh mobil, (c) kelajuan rata-rata, dan (d) kecepatan rata-rata mobil!
Solusi:
(a) Jarak total adalah luas di bawah grafik v-t:
(d) Kecepatan rata-rata = 218 m/24 dtk = 9,08 m/dtk
Soal 7
Sebuah mobil bergerak dengan kelajuan 80 km/jam di kawasan sekolah. Seorang polisi lalulintas mempercepat sepeda motornya dari keadaan diam tepat setelah pengebut melewatinya dengan percepatan konstan setelah 8 km/jam.s. (a) kapan polisi menangkap pengebut itu? (b) berapa kecepatan berapa motor polisi ketika menangkap pengebut?
Solusi:
Persoalan ini lebih sulit karena ada dua benda yang bergerak. Kita ambil posisi awal kedua kendaraan itu sebagai titik asal, dengan arah positif searah dengan gerakan, dan menetapkan t = 0 (titik A) sebagai saat pengebut melewati sepeda motor polisi.
(a) Karena mobil bergerak dengan kecepatan tetap, posisinya xc (pengebut) diberikan olehxc = vot = (80 km/jam)t
posisi motor polisi xp diberikan oleh
xp = ½ at2 = ½(8 km/jam.s)t2
kita dapat menemukan waktu ketika kedua mobil berada pada posisi yang sama dengan mengambil xc = xp dan mencari t:
(80 km/jam)t = ½(8 km/jam.s)t2
t = 20 s
jadi, polisi dapat menangkap pengemut pada waktu 20 s.
(b) Kecepatan sepeda motor polisi adalahvp = vop + at = 0 + (8 km/jam.s)(20 s) = 160 km/jam
pada saat ini, kelajuan sepeda motor polisi dua kali kelajuan pengebut. Ini pasti benar karena kecepatan rata-rata sepeda motor polisi adalah separo dari kecepatan akhirnya, dan karena kedua kendaraan menempuh jarak yang sama, maka keduanya harus mempunyai kecepatan rata-rata yang sama. Gambar (4) menunjukkan grafik untuk kedua kendaraan.
Sebuah mobil bergerak lurus beraturan dan menempuh 3 km dalam waktu 2 menit. Berapa lama diperlukan mobil itu untuk menempuh 75 km?
Solusi:
Diketahui: x0 = 0; v = 3/2 km/menit dan x = 75 km.
pada gerak lurus dengan kecepatan tetap, berlaku
x = x0 + vt
75 km = 0 + (1,5 km/menit)t
t = 50 menit
Soal 2
Dua buah mobil yang terpisah sejauh 75 km bergerak saling mendekat, pada saat bersamaan, masing-masing dengan kecepatan 90 km/jam dan 60 km/jam. Kapan dan di mana kedua mobil tersebut berpapasan?
Solusi:
Cara I:
Jika kita ambil titik acuan di mobil A, maka: x0A = 0, vA = 90 km/jam; tA = tB = T (waktu bersamaan); vB = - 60 km/jam (minus karena ke kiri), x0B = 75 km.
Kedua mobil berpapasan jika posisi mobil A sama dengan posisi mobil B, yaitu:
xA = xB
x0A + vAtA = x0B + v0BtB
0 + (90 km/jam)T = 75 km + (- 60 km/jam)T
T = 0,5 jam (waktu kedua mobil berpapasan)
Posisi berpapasan dapat diperoleh dari
xA = x0A + vAtA = 0 + (90 km/jam)(0,5 jam) = 45 km dari mobil A mula-mula.
Cara II:
- Untuk mobil A, 90 km/jam artinya selama 1 jam menempuh jarak 90 km
- Untuk mobil B, 60 km/jam artinya selama 1 jam menempuh jarak 60 km
- Dalam 1 jam kedua mobil semakin mendekat 90 km + 60 km = 150 km
- Karena jarak mula-mula 75 km, maka waktu berpapasan adalah 75/150 = 0,5 jam
- Bertemu pada posisi 90 km/jam x 0,5 jam = 45 km dari posisi A mula-mula.
Sebuah mobil bergerak dengan kecepatan 27 km/jam, kemudian mobil ini dipercepat dengan percepatan 2 m/s2. Hitung kecepatan dan jarak yang ditempuh selama 5 detik setelah pemercepat itu.
Solusi:
Diketahui: v0 = 27 km/jam = 7,5 m/s; a = 2 m/s2; t = 5 s dan dan x0 = 0.
Dengan menggunakan,
v = v0 + at = 7,5 m/s + (2 m/s2)(5 s) = 17,5 m/s
dan x = x0 + v0t + ½ at2 = 0 + (7,5 m/s)(5 s) + ½ (2 m/s2)(5 s)2 = 62,5 m
Soal 4
Sebuah sepeda motor bergerak dengan kecepatan 54 km/jam. Tiba-tiba motor tersebut direm mendadak dan berhenti setelah 2 detik. Hitung jarak yang ditempuh motor tersebut selama pengereman.
Solusi:
v0 = 54 km/jam = 15 m/s; t = 2 s; x0 = 0; v = 0 (berhenti). Kita gunakan, x = 1/2 (v0 + v)t = 1/2 (15 m/s + 0) . 2 s = 15 m
Soal 5
Sebuah kereta api awalnya bergerak dengan kecepatan tetap 90 km/jam. Tiba-tiba kereta direm mendadak dengan perlambatan 8 m/s2. Setelah berapa detik kereta itu menempuh jarak 21 meter dari saat kereta tersebut direm.
Solusi
Diketahui: a = - 8 m/s2; x0 = 0; v0 = 90 km/jam = 25 m/s; x = 21 m, maka dengan
x = x0 + v0t + ½ at2
21 m = 0 + (25 m/s)t + ½ (-8 m/s2)t2
0 = 4t2 – 25t + 21
Atau 0 = (4t – 21)(t – 1)
t1 = 21/4 = 5,25 sekon; t2 = +1 sekon
kita disini mendapatkan dua hasil yang berbeda, hal ini bisa dijelaskan sebagai berikut: anggap P berjarak 21 m dari posisi kereta ketika direm. Pertama kali kereta melewati A dalam waktu 1 s namun karena kereta terus diperlambat, maka kecepatan kereta akhirnya negatif, kereta bergerak mundur dan akan kembali ke titik P setelah 5,25 sekon.
Soal 6
Gambar (2) di bawah ini merupakan grafik kecepatan versus waktu dari sebuah mobil yang bergerak sepanjang jalan lurus.
Tentukan: (a) jarak total yang ditempuh mobil tersebut, (b) perpindahan total yang ditempuh mobil, (c) kelajuan rata-rata, dan (d) kecepatan rata-rata mobil!
Solusi:
(a) Jarak total adalah luas di bawah grafik v-t:
- Dari 0 sampai 5 s: L1 = ½ (5 s)(20 m/s) = 50 m
- Dari 5 s sampai 8 s: L2 = 3 s/2 (20 m/s + 12 m/s) = 48 m
- Dari 8 s sampai 21 s: L3 = (12 m/s)(13 s + 10 s)/2 = 138 m
- Dari 21 s sampai 24 s: L4 = ½ (3 s)(12 m/s) = 18 m
- Jadi jarak total = luas total = 254 m
- Dari 0 sampai 5 s: L1 = ½ (5 s)(20 m/s) = 50 m
- Dari 5 s sampai 8 s: L2 = 3 s/2 (20 m/s + 12 m/s) = 48 m
- Dari 8 s sampai 21 s: L3 = (12 m/s)(13 s + 10 s)/2 = 138 m
- Dari 21 s sampai 24 s: L4 = ½ (3 s)(-12 m/s) = -18 m
- Jadi perpindahan total = luas total = 218 m
(d) Kecepatan rata-rata = 218 m/24 dtk = 9,08 m/dtk
Soal 7
Sebuah mobil bergerak dengan kelajuan 80 km/jam di kawasan sekolah. Seorang polisi lalulintas mempercepat sepeda motornya dari keadaan diam tepat setelah pengebut melewatinya dengan percepatan konstan setelah 8 km/jam.s. (a) kapan polisi menangkap pengebut itu? (b) berapa kecepatan berapa motor polisi ketika menangkap pengebut?
Solusi:
Persoalan ini lebih sulit karena ada dua benda yang bergerak. Kita ambil posisi awal kedua kendaraan itu sebagai titik asal, dengan arah positif searah dengan gerakan, dan menetapkan t = 0 (titik A) sebagai saat pengebut melewati sepeda motor polisi.
(a) Karena mobil bergerak dengan kecepatan tetap, posisinya xc (pengebut) diberikan olehxc = vot = (80 km/jam)t
posisi motor polisi xp diberikan oleh
xp = ½ at2 = ½(8 km/jam.s)t2
kita dapat menemukan waktu ketika kedua mobil berada pada posisi yang sama dengan mengambil xc = xp dan mencari t:
(80 km/jam)t = ½(8 km/jam.s)t2
t = 20 s
jadi, polisi dapat menangkap pengemut pada waktu 20 s.
(b) Kecepatan sepeda motor polisi adalahvp = vop + at = 0 + (8 km/jam.s)(20 s) = 160 km/jam
pada saat ini, kelajuan sepeda motor polisi dua kali kelajuan pengebut. Ini pasti benar karena kecepatan rata-rata sepeda motor polisi adalah separo dari kecepatan akhirnya, dan karena kedua kendaraan menempuh jarak yang sama, maka keduanya harus mempunyai kecepatan rata-rata yang sama. Gambar (4) menunjukkan grafik untuk kedua kendaraan.



Tidak ada komentar:
Posting Komentar