Pada halaman ini akan dibahas mengenai Contoh soal ggl induksi dan pembahasannya. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Soal 1
Sebuah kumparan dengan 50 lilitan, fluks magnetiknya meningkat dari 2,50 x 10-3Wb menjadi 1,250 x 10-2Wb dalam waktu 0,40 s. Hitung ggl induksi rata-rata dalam kumparan.
Jawab;
Jumah lilitan N = 50; fluks awal φ1 = 2,50 x 10-3Wb; fluks akhir φ2 = 1,25 x 10-2Wb; selang waktu ∆t = 0,40 s. Dalam kasus ini, ggl induksi ε ditimbulkan oleh laju perubahan fluks yang konstan, sehingga ε dihitung dengan
ε = ∆φ/∆t
= –N(φ2 – φ1)/∆t
ε = –50(1,25 x 10-2Wb – 2,5 x 10-3Wb)/0,40 s
= –1,25 Volt
Tanda negatif menyatakan bahwa fluks induksi berlawanan arah dengan fluks utama.
Soal 2
Sebuah kawat tertutup berbentuk persegi dengan luas 0,02 m2 diletakkan pada bidang datar. Medan magnet seragam diberikan pada bidang tersebut dengan arah menembus ke dalam bidang secara tegak lurus menjauhi pembaca. Medan magnet tersebut diturunkan dengan laju tetap 2 x 10-4 T/s. Jika hambatan kawat 0,1 Ω, tentukanlah bear dan arah arus induksi yang timbul.
Jawab;
Luas A = 0,02 m2; laju medan magnet B/t = 2 x 10-4T/s; dan hambatan R = 0,1 Ω, maka besar ggl induksi dalam kawat
ε = BA/t
= (2 x 10-4T/s)(0,02 m2) = 4 x 10-6 Volt
Maka arus linduksi dalam kawat adalah
I = ε/R = (4 x 10-6 V)/0,1Ω = 0,04 mA
Soal 3
Suatu kumparan 50 lilitan dengan diameter 8 cm ditempatkan dalam suatu medan magnetik 1 T yang diarahkan tegak lurus bidang penampang kumparan. Dari t = 0 medan magnetik mulai dinaikkan dengan laju tetap dan mencapai besar 1,3 T dalam waktu 10 detik. Setelah itu medan konstan. Berapa induksi magnetik dalam kumparan pada t ≤ 0, t = 5,0 s, = 5,0 s, t ≥ 10 s?
Jawab;
Pada t ≤ 0 medan konstan sehingga ggl induksi nol, demikian juga pada t ≥ 10 s gglnya juga nol. Ggl induksi tidak nol ketika terjadi perubahan fluks magnetik dan ini terjadi pada 0 < t < 10 s.
Fluks mula-mula adalah
φ0 = B0A = B0(¼πd2)
fluks akhirnya adalah
φ = BA = B(¼πd2)
jadi perubahan fluksnya adalah
∆φ = φ – φ0 = ¼πd2(B – B0)
Ggl induksi dapat dicari dengan persamaan
ε = –N ∆φ/∆t
= –Nπd2(B – B0)/4∆t
ε = –50π(0,08 m)2(1,3 T – 1 T)/4.10
= –7,54 x 10-3 Volt
Jadi, dapat disimpulkan;
t ≤ 0, ggl induksinya ε = 0,
t = 5 detik, ggl induksinya = 7,54 x 10-3 Volt
t ≥ 10 detik, ggl induksinya ε = 0
Soal 4
Suatu kumparan kawat yang terdiri dari 30 lilitan mempunyai luas penampang 4cm2. Hambatan kawat 20 Ω. Bidang kumparan tegak lurus medan magnetik yang besarnya 1 T. Tiba-tiba kumparan diputar sebesar 600. Berapakah banyak muatan yang lewat pada suatu titik dalam kumparan ini selama waktu kumparan ini diputar?
Jawab;
Ketika kumparan diputar terjadilah perubahan fluks yang masuk dalam kumparan. Fluks mula-mula (ketika vektor normal bidang sejajar dengan medan magnetik) adalah
φ0 = BA cos 00 = BA
fluks akhir (ketika vektor normal bidang membentuk sudut 600 dengan medan magnetik);
φ0 = BA cos 600 = BA/2
Jadi, laju perubahan fluks adalah
∆φ/∆t = (BA/2 – BA)/∆t = –BA/2∆t
Ggl induksi dicari dengan hukum Faraday;
ε = –N ∆φ/∆t
= NBA/2∆t
Arus induksi dicari dengan persamaan
i = ε/R = NBA/2R∆t
Maka muatan yang mengaling dalam waktu ∆t adalah
Q = i∆t = NBA/2R
Karena B = 1 T; A = 4 cm2 = 4 x 10-4 m2; R = 2Ω dan N = 30 lilitan, maka
Q = (30)(1 T)(4 x 10-4 m2)/2(2Ω)
Q = 300 μC
Soal 5
Suatu kumparan terdiri dari 50 lilitan digerakan ke suatu bidang di mana terdapat medan magnetik dengan kekuatan 6 kilogauss. Panjang sisi kumparan 10 cm dan hambatannya 0,75 ohm. Jika kecepatan gerak kumparan itu 2 cm/s, berapakah kuat arus yang melalui kumparan kawat itu (a) sebelum kumparan mencapai bidang bermagnet, (b) ketika kumparan meninggalkan bidang dan (c) setelah kumparan melewati bidang.
Jawab;
Sebelum kumparan memasuki bidang medan magnet, tidak ada fluks magnetik sehingga arus induksinya nol. Demikian juga setelah kumparan meninggalkan bidang medan magnet.
Ketika kumparan mulai meninggalkan bidang, terjadilah perubahan fluks yang memasuki kumparan. Perubahan fluks ini menimbulkan ggl induksi.
Misalkan panjang sisi kumparan l, sehigga fluks mula-mula (sesaat sebelum meninggalkan bidang medan magnet) adalah
φ0 = BA = Bl2
Misalkan setelah waktu ∆t kumparan telah bergerak sejauh ∆x = v∆t sehingga bidang yang ditembus medan magnetik adalah seluas l2 – l∆x. Fluks yang menembus kumparan adalah
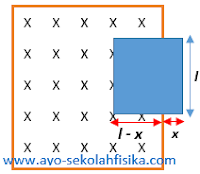φ = BA’ = B(l2 – l∆x) = Bl2 – Bl∆x
Jadi laju perubahan fluks adalah
φ/∆t = (Bl2 – Bl∆x)/∆t
φ/∆t = –Blv
ggl induksi dicari dengan hukum Faraday
ε = –N ∆φ/∆t
ε = NBlv
Jadi, arus induksi yang mengalir pada kumparan adalah
I = ε/R = NBlv/R
Karena, B = 6 kilogauss = 6 x 103 gauss = 0,6 T; R = 0,75 ohm; N = 50; v = 2 cm/s = 0,02 m/s dan l = 10 cm = 0,1 m.
I = NBlv/R
= 50(0,1 T)(0,1 m)(0,02 m/s)/0,75 ohm
I = 0,08A
Soal 6
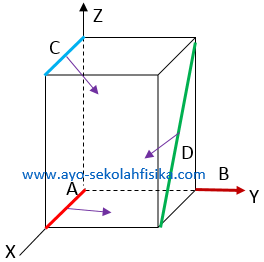
Kubus pada gambar berikut mempunyai rusuk 1 m berada dalam medan magnetik homogen 0,2 T, berarah sepanjang sumbu Y positif. Kawat A, C dan D bergerak dalam arah seperti gambar, masing-masing dengan kecepatan 0,5 m/s. (a) Tentukan ggl induksi antara ujung-ujungsetiap kawat dan (b) tentukan beda potensial antara ujung-ujung setiap kawat.
Jawab;
Perhatikan gambar di bawah ini,
(a) Panjang rusuk a = 1 m; panjang kawat lA = a = 1 m; panjang kawat lC = a = 1 m; panjang kawat lD = a√2 = √2 m; besar induksi magnetik B = 0,2 T; kelajuan v = 0,5 m/s.
Kawat A, θ = ∠(v,B) = 00,
εA = Blv sin θ = (0,2 T)(1 m)(0,5 m/s)(0) = 0
Kawat D, θ = ∠(v,B) = 900,
εD = Blv sin θ = (0,2 T) (√2 m)(0,5 m/s)(1) = 0,1√2 Volt
Kawat C, θ = ∠(v,B) = 450,
εC = Blv sin θ = (0,2 T)(1 m)(0,5 m/s)(½√2) = 0,05√2 Volt
(b) beda potensial antara ujung-ujung setiap kawat = ggl yang timbul pada ujung-ujung kawat. Dengan demikian,
Beda potensial kawat A, VA = εA = 0
Beda potensial kawat D, VD = εD = 0,1√2 Volt
Beda potensial kawat C, VC = εC = 0,05√2 Volt
Soal 7
Luas penampang kumparan tertutup yang memiliki 20 lilitan adalah 1,5 cm2 dan hambatannya 9,0 Ω. Kumparan dihubungkan ke suatu instrumen pengukur muatan (hambatan dalam = 16,0 Ω) melalui timah solderan (hambatan dapat diabaikan). Tentukan besar muatan listrik induksi ketika kumparan ditarik dengan cepat keluar dari daerah di mana B = 1,80 T ke suatu titik di mana B adalah nol. Bidang kumparan ketika berada dalam medan magnetik adalah tegak lurus terhadap medan magnetik.
Jawab;
Jumlah lilitan N = 20; luas bidang kumparan A = 1,50 x 10-4 m2, hambatan kumparan R1 = 9,0 Ω; hambatan dalam R2 = 16,0 Ω maka hambatan total R = R1 + R2 = 25,0 Ω; medan magnet awal B1 = 1,8 T dan medan magnet akhir B2 = 0.
Karena bidang kumparan tegak lurus terhadap medan magnetik dan ggl induksi, ε, ditimbulkan oleh laju perubahan induksi magnetik yang konstan, maka ggl dihitung dengan persamaan,
ε = –NA∆B/∆t
Arus induksi iind melalui rangkaian dengan hambatan total R adalah
iind = ε/R = –NA∆B/R∆t
besar muatan listrik induksi qind adalah
qind = iind∆t = –NA∆B/R
qind = –(20)(1,5 x 10-4 m2)(0 – 1,80 T)/25,0 Ω = 216 μC
Soal 8
Suatu kumparan persegi panjang memiliki dimensi 0,3 m x 0,4 m dan 200 lilitan berputar terhadap suatu poros yang sejajar dengan sisi panjangnya. Kumparan membuat 3000 putaran per menit dalam suatu medan magnetik homogen 0,08 tesla. Hitung ggl induksi sesaat ketika bidang kumparan membuat sudut; (a) 00; (b) 600 dan (c) 900 terhadap arah medan magnetik.
Jawab;
Luas bidang kumparan A = 0,3 m x 0,4 m = 0,12 m2; jumlah lilitan N = 200; frekuensi sudut ω = 3000 putaran/menit = 100π rad/s; induksi magnetik B = 0,08 T.
HATI-HATI; suduat θ adalah sudut antara normal bidang kumparan n dengan arah medan magnetik B dan sudut α adalah sudut antara bidang kumparan dengan B, maka berlaku θ = 90 – α.
Di sini ggl induksi dibangkitkan oleh perubahan sudut θ akibat kumparan diputar terhadap poros yang terletak pada bidang kumparan, sesuai dengan prinsip generator, sehingga ggl dihitung dengan
ε = εm sin θ dengan
εm = NBAω
= (200)(0,08 T)(0,12 m2)(100π rad/s) = 192π volt
(a) α = 00; θ = 900 – α = 900 maka,
ε = εm sin θ = 192π volt
(b) α = 600; θ = 900 – α = 300 maka,
ε = εm sin θ = (192π volt)(sin 300) = 96π volt
(c) α = 900; θ = 900 – α = 00 maka,
ε = εm sin θ = (192π volt)(sin 00) = 0
Soal 9
Suatu kumparan datar persegi panjang dengan ukuran 2,0 cm x 3,0 cm dan 60 lilitan dihubungkan ke suatu galvanometer pengukur muatan listrik. Hambatan total rangkaian adalah 100 ohm. Kedudukan bidang kumparan mula-mula tegak lurus terhadap suatu medan magnetik homogen dengan rapat fluks 0,30 T. Hitung muatan listrik yang akan ditunjukkan oleh galvanometer jika kumparan diputar melalui sudut (a) 600 dan (b) 900.
Jawab;
Luas bidang kumparan A = 0,02 cm x 0,03 m = 0,0006 m2; jumlah lilitan N = 60; hambatan rangkaian = 100 ohm; induksi magnetik B = 0,30 T. Kedudukan kumparan mula-mula tegak lurus medan magnetik ∠(n,B) = θ1 = 00, cos θ1 = 1.
(a) kedudukan kumparan setelah diputar θ2 = 600, maka ggl induksinya
ε = –NBA ∆cos θ/∆t
= –NBA (cos θ2 – cos θ1)/∆t
Karena ε = IR, maka
I∆t = –NBA (cos θ2 – cos θ1)/R
Maka muatan listrik yang kita peroleh adalah
q = –NBA (cos θ2 – cos θ1)/R
= –(60)(0,3 T)(0,0006 m2)(cos 600 – cos 00)/(100 ohm)
q = 54μC
(a) kedudukan kumparan setelah diputar θ2 = 900, maka ggl induksinya
q = –NBA (cos θ2 – cos θ1)/R
= –(60)(0,3 T)(0,0006 m2)(cos 900 – cos 00)/(100 ohm)
q = 108μC
Sebuah kumparan dengan 50 lilitan, fluks magnetiknya meningkat dari 2,50 x 10-3Wb menjadi 1,250 x 10-2Wb dalam waktu 0,40 s. Hitung ggl induksi rata-rata dalam kumparan.
Jawab;
Jumah lilitan N = 50; fluks awal φ1 = 2,50 x 10-3Wb; fluks akhir φ2 = 1,25 x 10-2Wb; selang waktu ∆t = 0,40 s. Dalam kasus ini, ggl induksi ε ditimbulkan oleh laju perubahan fluks yang konstan, sehingga ε dihitung dengan
ε = ∆φ/∆t
= –N(φ2 – φ1)/∆t
ε = –50(1,25 x 10-2Wb – 2,5 x 10-3Wb)/0,40 s
= –1,25 Volt
Tanda negatif menyatakan bahwa fluks induksi berlawanan arah dengan fluks utama.
Soal 2
Sebuah kawat tertutup berbentuk persegi dengan luas 0,02 m2 diletakkan pada bidang datar. Medan magnet seragam diberikan pada bidang tersebut dengan arah menembus ke dalam bidang secara tegak lurus menjauhi pembaca. Medan magnet tersebut diturunkan dengan laju tetap 2 x 10-4 T/s. Jika hambatan kawat 0,1 Ω, tentukanlah bear dan arah arus induksi yang timbul.
Jawab;
Luas A = 0,02 m2; laju medan magnet B/t = 2 x 10-4T/s; dan hambatan R = 0,1 Ω, maka besar ggl induksi dalam kawat
ε = BA/t
= (2 x 10-4T/s)(0,02 m2) = 4 x 10-6 Volt
Maka arus linduksi dalam kawat adalah
I = ε/R = (4 x 10-6 V)/0,1Ω = 0,04 mA
Soal 3
Suatu kumparan 50 lilitan dengan diameter 8 cm ditempatkan dalam suatu medan magnetik 1 T yang diarahkan tegak lurus bidang penampang kumparan. Dari t = 0 medan magnetik mulai dinaikkan dengan laju tetap dan mencapai besar 1,3 T dalam waktu 10 detik. Setelah itu medan konstan. Berapa induksi magnetik dalam kumparan pada t ≤ 0, t = 5,0 s, = 5,0 s, t ≥ 10 s?
Jawab;
Pada t ≤ 0 medan konstan sehingga ggl induksi nol, demikian juga pada t ≥ 10 s gglnya juga nol. Ggl induksi tidak nol ketika terjadi perubahan fluks magnetik dan ini terjadi pada 0 < t < 10 s.
Fluks mula-mula adalah
φ0 = B0A = B0(¼πd2)
fluks akhirnya adalah
φ = BA = B(¼πd2)
jadi perubahan fluksnya adalah
∆φ = φ – φ0 = ¼πd2(B – B0)
Ggl induksi dapat dicari dengan persamaan
ε = –N ∆φ/∆t
= –Nπd2(B – B0)/4∆t
ε = –50π(0,08 m)2(1,3 T – 1 T)/4.10
= –7,54 x 10-3 Volt
Jadi, dapat disimpulkan;
t ≤ 0, ggl induksinya ε = 0,
t = 5 detik, ggl induksinya = 7,54 x 10-3 Volt
t ≥ 10 detik, ggl induksinya ε = 0
Soal 4
Suatu kumparan kawat yang terdiri dari 30 lilitan mempunyai luas penampang 4cm2. Hambatan kawat 20 Ω. Bidang kumparan tegak lurus medan magnetik yang besarnya 1 T. Tiba-tiba kumparan diputar sebesar 600. Berapakah banyak muatan yang lewat pada suatu titik dalam kumparan ini selama waktu kumparan ini diputar?
Jawab;
Ketika kumparan diputar terjadilah perubahan fluks yang masuk dalam kumparan. Fluks mula-mula (ketika vektor normal bidang sejajar dengan medan magnetik) adalah
φ0 = BA cos 00 = BA
fluks akhir (ketika vektor normal bidang membentuk sudut 600 dengan medan magnetik);
φ0 = BA cos 600 = BA/2
Jadi, laju perubahan fluks adalah
∆φ/∆t = (BA/2 – BA)/∆t = –BA/2∆t
Ggl induksi dicari dengan hukum Faraday;
ε = –N ∆φ/∆t
= NBA/2∆t
Arus induksi dicari dengan persamaan
i = ε/R = NBA/2R∆t
Maka muatan yang mengaling dalam waktu ∆t adalah
Q = i∆t = NBA/2R
Karena B = 1 T; A = 4 cm2 = 4 x 10-4 m2; R = 2Ω dan N = 30 lilitan, maka
Q = (30)(1 T)(4 x 10-4 m2)/2(2Ω)
Q = 300 μC
Soal 5
Suatu kumparan terdiri dari 50 lilitan digerakan ke suatu bidang di mana terdapat medan magnetik dengan kekuatan 6 kilogauss. Panjang sisi kumparan 10 cm dan hambatannya 0,75 ohm. Jika kecepatan gerak kumparan itu 2 cm/s, berapakah kuat arus yang melalui kumparan kawat itu (a) sebelum kumparan mencapai bidang bermagnet, (b) ketika kumparan meninggalkan bidang dan (c) setelah kumparan melewati bidang.
Sebelum kumparan memasuki bidang medan magnet, tidak ada fluks magnetik sehingga arus induksinya nol. Demikian juga setelah kumparan meninggalkan bidang medan magnet.
Ketika kumparan mulai meninggalkan bidang, terjadilah perubahan fluks yang memasuki kumparan. Perubahan fluks ini menimbulkan ggl induksi.
Misalkan panjang sisi kumparan l, sehigga fluks mula-mula (sesaat sebelum meninggalkan bidang medan magnet) adalah
φ0 = BA = Bl2
Misalkan setelah waktu ∆t kumparan telah bergerak sejauh ∆x = v∆t sehingga bidang yang ditembus medan magnetik adalah seluas l2 – l∆x. Fluks yang menembus kumparan adalah
φ = BA’ = B(l2 – l∆x) = Bl2 – Bl∆xJadi laju perubahan fluks adalah
φ/∆t = (Bl2 – Bl∆x)/∆t
φ/∆t = –Blv
ggl induksi dicari dengan hukum Faraday
ε = –N ∆φ/∆t
ε = NBlv
Jadi, arus induksi yang mengalir pada kumparan adalah
I = ε/R = NBlv/R
Karena, B = 6 kilogauss = 6 x 103 gauss = 0,6 T; R = 0,75 ohm; N = 50; v = 2 cm/s = 0,02 m/s dan l = 10 cm = 0,1 m.
I = NBlv/R
= 50(0,1 T)(0,1 m)(0,02 m/s)/0,75 ohm
I = 0,08A
Soal 6
Kubus pada gambar berikut mempunyai rusuk 1 m berada dalam medan magnetik homogen 0,2 T, berarah sepanjang sumbu Y positif. Kawat A, C dan D bergerak dalam arah seperti gambar, masing-masing dengan kecepatan 0,5 m/s. (a) Tentukan ggl induksi antara ujung-ujungsetiap kawat dan (b) tentukan beda potensial antara ujung-ujung setiap kawat.
Perhatikan gambar di bawah ini,
Kawat A, θ = ∠(v,B) = 00,
εA = Blv sin θ = (0,2 T)(1 m)(0,5 m/s)(0) = 0
Kawat D, θ = ∠(v,B) = 900,
εD = Blv sin θ = (0,2 T) (√2 m)(0,5 m/s)(1) = 0,1√2 Volt
Kawat C, θ = ∠(v,B) = 450,
εC = Blv sin θ = (0,2 T)(1 m)(0,5 m/s)(½√2) = 0,05√2 Volt
(b) beda potensial antara ujung-ujung setiap kawat = ggl yang timbul pada ujung-ujung kawat. Dengan demikian,
Beda potensial kawat A, VA = εA = 0
Beda potensial kawat D, VD = εD = 0,1√2 Volt
Beda potensial kawat C, VC = εC = 0,05√2 Volt
Soal 7
Luas penampang kumparan tertutup yang memiliki 20 lilitan adalah 1,5 cm2 dan hambatannya 9,0 Ω. Kumparan dihubungkan ke suatu instrumen pengukur muatan (hambatan dalam = 16,0 Ω) melalui timah solderan (hambatan dapat diabaikan). Tentukan besar muatan listrik induksi ketika kumparan ditarik dengan cepat keluar dari daerah di mana B = 1,80 T ke suatu titik di mana B adalah nol. Bidang kumparan ketika berada dalam medan magnetik adalah tegak lurus terhadap medan magnetik.
Jawab;
Jumlah lilitan N = 20; luas bidang kumparan A = 1,50 x 10-4 m2, hambatan kumparan R1 = 9,0 Ω; hambatan dalam R2 = 16,0 Ω maka hambatan total R = R1 + R2 = 25,0 Ω; medan magnet awal B1 = 1,8 T dan medan magnet akhir B2 = 0.
Karena bidang kumparan tegak lurus terhadap medan magnetik dan ggl induksi, ε, ditimbulkan oleh laju perubahan induksi magnetik yang konstan, maka ggl dihitung dengan persamaan,
ε = –NA∆B/∆t
Arus induksi iind melalui rangkaian dengan hambatan total R adalah
iind = ε/R = –NA∆B/R∆t
besar muatan listrik induksi qind adalah
qind = iind∆t = –NA∆B/R
qind = –(20)(1,5 x 10-4 m2)(0 – 1,80 T)/25,0 Ω = 216 μC
Soal 8
Suatu kumparan persegi panjang memiliki dimensi 0,3 m x 0,4 m dan 200 lilitan berputar terhadap suatu poros yang sejajar dengan sisi panjangnya. Kumparan membuat 3000 putaran per menit dalam suatu medan magnetik homogen 0,08 tesla. Hitung ggl induksi sesaat ketika bidang kumparan membuat sudut; (a) 00; (b) 600 dan (c) 900 terhadap arah medan magnetik.
Jawab;
Luas bidang kumparan A = 0,3 m x 0,4 m = 0,12 m2; jumlah lilitan N = 200; frekuensi sudut ω = 3000 putaran/menit = 100π rad/s; induksi magnetik B = 0,08 T.
HATI-HATI; suduat θ adalah sudut antara normal bidang kumparan n dengan arah medan magnetik B dan sudut α adalah sudut antara bidang kumparan dengan B, maka berlaku θ = 90 – α.
Di sini ggl induksi dibangkitkan oleh perubahan sudut θ akibat kumparan diputar terhadap poros yang terletak pada bidang kumparan, sesuai dengan prinsip generator, sehingga ggl dihitung dengan
ε = εm sin θ dengan
εm = NBAω
= (200)(0,08 T)(0,12 m2)(100π rad/s) = 192π volt
(a) α = 00; θ = 900 – α = 900 maka,
ε = εm sin θ = 192π volt
(b) α = 600; θ = 900 – α = 300 maka,
ε = εm sin θ = (192π volt)(sin 300) = 96π volt
(c) α = 900; θ = 900 – α = 00 maka,
ε = εm sin θ = (192π volt)(sin 00) = 0
Soal 9
Suatu kumparan datar persegi panjang dengan ukuran 2,0 cm x 3,0 cm dan 60 lilitan dihubungkan ke suatu galvanometer pengukur muatan listrik. Hambatan total rangkaian adalah 100 ohm. Kedudukan bidang kumparan mula-mula tegak lurus terhadap suatu medan magnetik homogen dengan rapat fluks 0,30 T. Hitung muatan listrik yang akan ditunjukkan oleh galvanometer jika kumparan diputar melalui sudut (a) 600 dan (b) 900.
Jawab;
Luas bidang kumparan A = 0,02 cm x 0,03 m = 0,0006 m2; jumlah lilitan N = 60; hambatan rangkaian = 100 ohm; induksi magnetik B = 0,30 T. Kedudukan kumparan mula-mula tegak lurus medan magnetik ∠(n,B) = θ1 = 00, cos θ1 = 1.
(a) kedudukan kumparan setelah diputar θ2 = 600, maka ggl induksinya
ε = –NBA ∆cos θ/∆t
= –NBA (cos θ2 – cos θ1)/∆t
Karena ε = IR, maka
I∆t = –NBA (cos θ2 – cos θ1)/R
Maka muatan listrik yang kita peroleh adalah
q = –NBA (cos θ2 – cos θ1)/R
= –(60)(0,3 T)(0,0006 m2)(cos 600 – cos 00)/(100 ohm)
q = 54μC
(a) kedudukan kumparan setelah diputar θ2 = 900, maka ggl induksinya
q = –NBA (cos θ2 – cos θ1)/R
= –(60)(0,3 T)(0,0006 m2)(cos 900 – cos 00)/(100 ohm)
q = 108μC
Tidak ada komentar:
Posting Komentar