Pada halaman ini akan dibahas mengenai Soal dan penyelesaian elastisitas zat padat. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Soal 1
Sebuah bahan baja yang akan digunakan untuk jembatan gantung memiliki modulus Young 2,0 x 1011 N/m2. Untuk menahan berat jembatan beberapa buah batang baja yang berbentuk silinder yang masing-masing luas penampangnya 8 cm2 dan panjangnya 50 m. Setiap batang ditarik dengan gaya 4,0 x 104 N. Tentukan: (a) tegangan, (b) pertambahan panjang dan (c) regangan yang dialami batang
Sebuah bahan baja yang akan digunakan untuk jembatan gantung memiliki modulus Young 2,0 x 1011 N/m2. Untuk menahan berat jembatan beberapa buah batang baja yang berbentuk silinder yang masing-masing luas penampangnya 8 cm2 dan panjangnya 50 m. Setiap batang ditarik dengan gaya 4,0 x 104 N. Tentukan: (a) tegangan, (b) pertambahan panjang dan (c) regangan yang dialami batang
Jawab
Diketahui: E = 2,0 x 1011 N/m2; A = 8 cm2 = 8 x 10-4 m2, l0 = 50 m, dan F = 4 x 104 N, maka
Diketahui: E = 2,0 x 1011 N/m2; A = 8 cm2 = 8 x 10-4 m2, l0 = 50 m, dan F = 4 x 104 N, maka
(a) Tegangan (σ)
(b) Pertambahan panjang batang (Δl)
(c) Regangan (e)
Soal 2:Sebuah kawat tembaga dan kawat baja dengan panjang yang sama dan penampang melintang yang sama digabungkan dari ujung ke ujung untuk membentuk kawat gabungan. Kawat gabungan tergantung dari dukungan yang kaku dan beban digantungkan dari ujung yang lain. Jika pertambahan panjang kabel gabungan adalah 2,4 mm, lalu berapa jumlah pertambahan panjang kawat baja dan kawat tembaga? (Ytembaga = 10 × 1010 N/m2, Ybaja = 2 × 1011 N/m2)
Jawab:
Ltembaga = Lbaja = L
Atembaga = Abaja = A
ΔLtotal = 2,4 mm
Dan ΔLtotal = ΔLtembaga + ΔLbaja
Persamaan modulus Young bahan elastis adalah
Y = FL/ΔLA atau ΔL = YA/FL sehingga
ΔLtembaga = Ytembaga A/FL dan
ΔLbaja = Ybaja A/FL
ΔLtembaga/ΔLbaja = Ytembaga/Ybaja = (10 × 1010 N/m2)/(2 × 1011 N/m2) = 0,5
Atau ΔLtembaga = 0,5ΔLbaja
Karena ΔLtotal = ΔLtembaga + ΔLbaja = 2,4 mm
1,5ΔLbaja = 2,4 mm
ΔLbaja = 1,6 mm
Dan ΔLtembaga = 0,5ΔLbaja = 0,5 x 1,6 mm = 0,8 mm
Soal 3
Batang baja dengan panjang l1 = 30 cm dan dua batang kuningan yang identik dengan panjang l2 = 20 cm masing-masing mendukung platform horisontal ringan seperti yang ditunjukkan pada gambar. Luas penampang masing-masing dari tiga batang adalah A = 1 cm2. Gaya vertikal ke bawah F = 5000 N diterapkan pada platform. Modulus elastisitas untuk baja Ybaja = 2 × 1011Nm-2 dan kuningan Ykuningan = 1 × 1011Nm-2. Tentukan tegangan kawat baja!
Jawab:
pertambahan panjang Δl = FL/AY maka F = AYΔL/L,Maka Persamaan Fbaja = AbYbΔLb/Lb,
Dan Fkuningan = AkYkΔLk/Lk
Pertambahan panjang untuk masing-masing batang sama, maka berlaku
Fkuningan + Fbaja + Fkuningan = F
2Fkuningan + Fbaja = F
Ab = Ak = 10-4 m2
Lb = 0,3 m dan Lk = 0,2 m
Ybaja = 2 × 1011Nm-2 dan Ykuningan = 1 × 1011Nm-2, sehingga
2 AkYkΔL/Lk + AbYbΔL/Lb = 5000
Diperoleh ΔL = 0,03 mm, maka tegangan yang dialami kuningan baja adalah
σb = F/regangan = 5000 N/(0,03 mm/0,3 m) = 20 MPa
Soal 4:
Sebuah batang ringan AB memiliki panjang 2 m tergantung horizontal oleh dua kawat seperti gambar. Satu kawat baja yang memiliki luas penampang 0,1 cm2 dan kawat yang lainnya dalah kuningan dengan luas penampang 0,2 cm2. Modulus Young kuningan 1,0 x 1011 N/m2 dan baja 2,0 x 1011 N/m2. Sebuah benda dengan berat W digantung pada titik C pada jarak x dari A. Tentukan x di mana tegangan kedua kawat sama besar!
Jawab:
Diketahu: Panjang batang d = 2 m, luas penampang baja, Ab = 0,1 cm2, luas penampang kuningan Ak = 0,2 cm2, modulus Young kuningan Ek = 1,0 x 1011 N/m2 dan modulus Young baja Eb = 2,0 x 1011 N/m2.Persamaan tegangan pada kawat adalah σ = F/A, maka=
σk = σb
Tk/Ak = Tb/Ab
Tk/Tb = Ak/Ab = (0,2 cm2)/( 0,1 cm2) = 2
Sistem dalam keadaan setimbang dengan mengambil poros di titik C maka
ΣτC = 0
Tbx = Tk (2 – x)
Tk/Tb = x/(2 – x)
2 = x/(2 – x)
x = 4/3 m dari A
Jadi beban W harus digantung pada posisi 4/3 m dari titik A agar tegangan kedua kawat sama besar.
Soal 5:
Kawat baja panjangnya2L dengan diameter d, luas penampang A kedua ujungnya diikat pada dinding seperti gambar. Benda bermassa m digantung pada tengah-tengah kawat yang membuat kawat meregang vertikal sejauh x. Jika modulus Young dari kawat adalah E, tentukan x!
Jawab:
System dalam keadaan setimbang maka
2T sin θ = mg
Karena θ sangan kecil maka
Sin θ = tan θ = θ = x/L
T = F = EAΔL/L
Karena ΔL = (x2 + L2)1/2 – L , maka
F = EA[(x2 + L2)1/2 – L]/L atau
F ≈ EAx2/L2
Tetapi
2T sin θ = mg
2[EAx2/L2][x/L] = mg
m = EAx3/gL3
Soal 6:
Kawat baja dengan luas penampang 3 x 10- 5m2 dan panjang 5 m meregang dengan panjang yang sama dengan kawat tembaga yang luas penampang 4,0 x 10-5m2 dan panjang 4 m. Jika beban yang diberikan pada kedua kawat sama besa, tentukan rasio modulus Young tembaga dengan baja?
Jawab:
Panjang kawat baja, L1 = 5 m, Luas penampang kawat baja, A1 = 3,0 × 10-5 m2 ,njang kawat tembaga, L2 = 4 m, Luas penampang kawat tembaga, A2 = 4,0 × 10-5 m2,
Perubahan panjang = ΔL1 = ΔL2 = ΔL
Biarkan gaya diterapkan di kedua situasi = F
Kita tahu, modulus Young dari kawat baja:
E1 = (F1/A1)(L1 /ΔL1)
= (F/3 x 10-5)(5/ΔL). . . . . . . . . . (1)
Juga, modulus Young dari kawat tembaga:
E2 = (F2/A2)(L2 /ΔL2)
= (F/4 × 10-5)(3/ΔL). . . . . . . . . . . (2)
Persamaan pembagi (1) dengan persamaan (2), kita mendapatkan:
E1/E2 = (5 × 4 × 10-5)/(3 × 10-5 × 4)
= 5 : 6
Rasio modulus Young dari baja terhadap modulus tembaga Young adalah 5 : 6
Soal 7:
Grafik yang diberikan di bawah ini adalah kurva tegangan-regangan suatu material. Tentukan (i) Perkiraan tegangan maksimum bahan ini (ii) modulus Young bahan ini!

Jawab:
dari kurva tegangan-regangan material,
(i) Dapat dilihat dari grafik bahwa perkiraan tegangan maksimum dari material ini adalah 300 × 106Nm-2 atau 3 × 108 N/m2.
(ii) diamati dari grafik yang diberikan bahwa untuk regangan 0,001, tegangan adalah 75 × 106N /m2. \
∴ Kita tahu, modulus Young, Y = Stress / Strain = 75 × 106/0.001 = 7.5 × 1010 Nm-2
Soal 8:
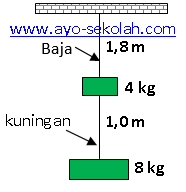
Kawat yang terbuat dari baja dan kuningan dan memiliki diameter 0,25 cm dimuat seperti yang digambarkan pada diagram di bawah ini. Panjang kawat kuningan adalah 1 m dan kawat bajanya adalah 1.8 m. Cari pertambahan pada kabel kuningan dan baja. (Ekuningan = 0,91 × 1011 N/m2, Ebaja = 2 × 1011 N/m2)
Jawab:
Mengingat, Diameter kawat, d = 0,25 m
Oleh karena itu, jari-jari kabel, r = d/2 = 0.125 cm
Panjang kawat baja, L1 = 1,8 m
Panjang kawat kuningan, L2 = 1,0 m
Total gaya yang diberikan pada kawat baja:
F1 = (4 + 8) g = 12 × 9,8 = 117,6 N
Kita tahu, modulus Young untuk baja:
E1 = (F1/A1)/(ΔL1/L1)
Dimana,ΔL1 = Ganti panjang kawat bajaA1 = Luas penampang kawat baja = πr12
Kita tahu, modulus Young dari baja, E1 = 2,0 × 1011 Pa
∴ ΔL1 = F1 × L1 / (A1 × E1)= (117,6 × 1,8)/[π (0.125 × 10-2) 2 × 2 × 1011] = 2.15 × 10-4m
Total gaya pada kawat kuningan:F2 = 8 × 9,8 = 78,4 N
Modulus Young untuk kuningan: E2 = 0,91 x 1011 Pa
Dimana,ΔL2 = Ganti panjang kawat kuningan
A1 = Luas penampang kawat kuningan = πr12
∴ ΔL2 = F2 × L2 / (A2 × E2)= (78,4 X 1)/[π × (0,12 × 10-2) 2 × (0,91 × 1011)] = 1,75 × 10-4 m
Oleh karena itu, pemanjangan kawat baja = 2.15 × 10-4m, dan Pemanjangan kawat kuningan = 1,75 × 10-4 m
Soal 9:
Massa 15 kg terikat pada kawat baja 1 m. Kemudian berputar dalam lingkaran vertikal dimana kecepatan sudutnya adalah 2 putaran/s. Jika luas penampang kawat adalah 0,060 cm2, tentukan pertambahan kawat bila benda berada pada titik terendah. (Ybaja = 2 × 1011 N/m2)
Jawab:
Massa, m = 15 kg
Panjang kawat, l = 1,0 m
kecepatan angular, ω = 2 putaran/s = 2 x 2π rad/s = 12,56 rad/s
Luas penampang kawat, A = 0,060 cm2 = 0,06 × 10-4m2
Pertambahan panjang kawat saat benda berada pada titik paling rendah.
Bila benda berada pada titik terendah lingkaran vertikal, gaya pada benda adalah:
F = mg + mlω2 = 15 × 9.8 + 15 × 1 × (12.56)2 = 2513.304 N
Kita tahu, modulus Young = Stress / StrainY = (F/A)/(Δl/l)∴ Δl = Fl/AY
Juga modulus muda untuk baja = 2 × 1011 Pa
=> Δl = (2513.304 × 1)/(0,06 × 10-4 × 2 × 1011) = 2,09 × 10-3 m
Karena itu, kenaikan kawat adalah 2,09 × 10-3 m.









Tidak ada komentar:
Posting Komentar