Pada halaman ini akan dibahas mengenai Penurunan Rumus Energi Kapasitor. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Penurunan Rumus Energi Kapasitor
Kapasitor adalah komponen listrik yang berfungsi untuk menyimpan muatan digambarkan terdiri dua plat lempeng sejajar yang memiliki luas lempeng A. Pada gambar dibawah digambarkan dua buah lempeng berwarna merah, lempeng sebelah kiri diberi muatan Positif Q dan lempeng sebelah kanan diberi muatan negatif Q, antara dua lempeng memiliki jarak pemisah sebesar d.
Kita lihat lagi gambaran kapasitor di bawah ini, karena lempeng sebelah kiri bermuatan positif dan lempeng sebelah kanan bermuatan negatif maka di dalam ruang antara kedua lempeng akan timbul medan listrik E seperti ditunjukan pada gambar berarah ke kanan.
Kita amati lagi gambaran kapasitor di atas pada kedua lempeng karena memiliki jenis muatan yang berbeda maka pada masing-masing lempeng akan timbul gaya listrik yang saling menarik, pada lempeng sebelah kiri yang bermuatan positif saya gambarkan timbul gaya listrik ke arah sebelah kanan F karena lempeng sebelah kiri akan ditarik oleh sebelah kanan.
Sebagaimana rumus usaha atau kerja
Dengan menggunakan rumus ini akan kita hitung besar energi yang tersimpan pada kapasitor. Gaya pada lempeng sebelah kiri bermuatan muatan listrik Q sama dengan besar muatan pada lempeng dikali besar medan listrik yang dihasilkan oleh lempeng negatif sebelah kanan, maka besar gaya bisa kita subtitusi dengan QE.
Sebagai catatan penting, medan listrik yang dipakai adalah medan listrik yang mengenai lempeng sebelah kiri berasal dari muatan lempeng sebelah kanan bermuatan -Q bukan medan listrik di dalam lempeng, karena menurut teorinya gaya akan timbul pada suatu muatan jika muatan itu menerima medan listrik yang berasal dari medan listrik luar. Besar medan listrik yang dihasilkan oleh satu lempeng dihitung dengan hukum Gauss yaitu
Kita subtitusikan persamaan medan listrik di dalam lempeng sejajar
Sigma adalag rapat muatan pada lempeng bisa kita subtitusi dengan Q/A
Persamaannya akan menjadi
Kemudian kita integralkan yang tidak lain dx adalah besar jarak d antara kedua lempeng. kita dapatkan persamaan energi menjadi
Kemudian kita subtitusi persamaan kapasitas kapasitor pada persamaan di atas
Dan kita dapatkan rumus energi kapasitor sebagai berikut
Kita bisa ubah rumus energi kapasitor dengan mensubtitusi persamaan muatan kapasitor
Kita bisa dapatkan bentuk lain rumus energi kapasitor
Persamaan energi ini bisa diartikan seberapa besar usaha yang dibutuhkan untuk menahan kedua lempeng tetap bearada pada jarak d.
Kapasitor adalah komponen listrik yang berfungsi untuk menyimpan muatan digambarkan terdiri dua plat lempeng sejajar yang memiliki luas lempeng A. Pada gambar dibawah digambarkan dua buah lempeng berwarna merah, lempeng sebelah kiri diberi muatan Positif Q dan lempeng sebelah kanan diberi muatan negatif Q, antara dua lempeng memiliki jarak pemisah sebesar d.
Kita lihat lagi gambaran kapasitor di bawah ini, karena lempeng sebelah kiri bermuatan positif dan lempeng sebelah kanan bermuatan negatif maka di dalam ruang antara kedua lempeng akan timbul medan listrik E seperti ditunjukan pada gambar berarah ke kanan.
Kita amati lagi gambaran kapasitor di atas pada kedua lempeng karena memiliki jenis muatan yang berbeda maka pada masing-masing lempeng akan timbul gaya listrik yang saling menarik, pada lempeng sebelah kiri yang bermuatan positif saya gambarkan timbul gaya listrik ke arah sebelah kanan F karena lempeng sebelah kiri akan ditarik oleh sebelah kanan.
Sebagaimana rumus usaha atau kerja
Dengan menggunakan rumus ini akan kita hitung besar energi yang tersimpan pada kapasitor. Gaya pada lempeng sebelah kiri bermuatan muatan listrik Q sama dengan besar muatan pada lempeng dikali besar medan listrik yang dihasilkan oleh lempeng negatif sebelah kanan, maka besar gaya bisa kita subtitusi dengan QE.
Sebagai catatan penting, medan listrik yang dipakai adalah medan listrik yang mengenai lempeng sebelah kiri berasal dari muatan lempeng sebelah kanan bermuatan -Q bukan medan listrik di dalam lempeng, karena menurut teorinya gaya akan timbul pada suatu muatan jika muatan itu menerima medan listrik yang berasal dari medan listrik luar. Besar medan listrik yang dihasilkan oleh satu lempeng dihitung dengan hukum Gauss yaitu
Kita subtitusikan persamaan medan listrik di dalam lempeng sejajar
Sigma adalag rapat muatan pada lempeng bisa kita subtitusi dengan Q/A
Persamaannya akan menjadi
Kemudian kita integralkan yang tidak lain dx adalah besar jarak d antara kedua lempeng. kita dapatkan persamaan energi menjadi
Kemudian kita subtitusi persamaan kapasitas kapasitor pada persamaan di atas
Dan kita dapatkan rumus energi kapasitor sebagai berikut
Kita bisa ubah rumus energi kapasitor dengan mensubtitusi persamaan muatan kapasitor
Kita bisa dapatkan bentuk lain rumus energi kapasitor
Persamaan energi ini bisa diartikan seberapa besar usaha yang dibutuhkan untuk menahan kedua lempeng tetap bearada pada jarak d.








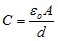




Tidak ada komentar:
Posting Komentar