Pada halaman ini akan dibahas mengenai Contoh Soal Vektor dan Pembahasannya. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Contoh Soal Vektor dan Pembahasanya
1. Diketahui dua buah vektor A dan B seperti terlihat pada gambar di bawah ini, besar vektor A 2 N dan besar vektor B 4 N.
Tentukan besar resultan vektor :
a.
b.
c.
Jawab
a. menentukan besar resultan
Untuk menjawab oprasi penjumlahan vektor ini kita harus gambar resultan vektor dengan cara menyatukan pangkal kedua vektor di satu titik seperti pada gambar 1 di bawah ini, resultan R bisa digambarkan dengan metode jajaran genjang seperti pada gambar 1. sudut
adalah sudur antara vektor A dan vektor B
Secara umum persamaan untuk menentukan besar resultan 2 buah vektor adalah
Kemudian bisa kita subtitusikan besar vektor dan besar dudut antara kedua vektor kemudian kita hitung
Besar resultan penjumlahan kedua vektor untuk soal nomor satu ini adalah
b. Menentukan resultan
Cara pertama
Untuk menghitung resultan pada nomor 1b ini sama seperti 1a tetapi karena vektor B negatif maka rah vektor menjadi kebalikan vektor B apada soal, kemudian kita satukan pangkal vektor A dan Pangkal vektor -B, dan kita bisa menentukan gambar resultan dengan metode jajaran genjang seperti pada gambar 2 di bawah ini.
Menghitung resultan vektor soal 1b menggunakan rumus resultan yang sama dengan rumus resultan 1a bedanya terdapat pada sudut antara kedua vektor, untuk soal 1b besar sudut antara vektor A dan vektor -B adalah
.
Besar resultanadalah
Cara kedua
Cara kedua untuk menentukan besar resultan adalah dengan menggunakan persamaan
Bedanya sudut yang kita gunakan menggunakan sudut yang sama seperti pada soal 1a yaitu
.
c. Menentukan resultan
Cara Pertama
Untuk menghitung resultan pada nomor 1c ini sama seperti 1a tetapi karena vektor A negatif maka arah vektor menjadi kebalikan vektor A apada soal, kemudian kita satukan pangkal vektor -A dan Pangkal vektor B, dan kita bisa menentukan gambar resultan dengan metode jajaran genjang seperti pada gambar 3 di bawah ini.
Menghitung resultan vektor soal 1c menggunakan rumus resultan yang sama dengan rumus resultan 1a bedanya terdapat pada sudut antara keduavektor, untuk soal 1c besar sudut antara vektor -A dan vektor B adalah .
Besar resultanadalah
Cara kedua
Cara kedua untuk menentukan besar resultanadalah dengan menggunakan persamaan
Bedanya sudut yang kita gunakan menggunakan sudut yang sama seperti pada soal 1a yaitu .
2. Terdapat tiga buah vektor gaya dengan besar vektor gaya pertama adalah 4 N, Besar vektor kedua adalah 6 N, dan besar vektor gaya ketiga adalah 6 N. Arah vektor pertama searah dengan sumbu x positif, arah vektor keduaterhadap garis sumbu x positif, arah vektor ketiga terhadap arah garis sumbu x negatif seperti pada gambar di bawah ini.
Besar resultan ketiga vektor gaya tersebut adalah ?
Jawab
Untuk menjawab persoalan menentukan besar resultan vektor yang berasal dari lebih dari dua vektor kita harus membuat komponen- komponen vektor pada sumbu x dan pada sumbu y untuk vektor-vektor yang tidak searah dengan sumbu x dan sumbu y. Pada soal nomor dua ini terdapat dua buah vektor yang harus dibuat komponennya karena tidak searah dengan sumbu x dan sumbu y yaitu vektor gaya kedua dan vektor gaya ketiga. Komponen-komponen vektor di gambarkan di bawah ini
Gaya pertama tidak perlu dibuat komponen vektornya karena sudah seraah dengan sumbu x positif. Langkah selanjutnya Jumlahkan gaya-gaya yang searah sumbu x, gaya searah sumbu x positif bernilai positif dan gaya yang searah sumbu x negatif bernilai negatif.
Resultan gaya yang searah sumbu x adalah
Jumlahkan gaya-gaya yang searah dengan sumbu y, gaya searah sumbu y positif bernilai positif dan gaya yang searah sumbu y negatif bernilai negatif.
Resultan gaya yang searah sumbu y adalah
Artinya dari tiga vektor yang ada pada persoalan sekarang hanya tinggal 2 vektor seperti pada gambar di bawah ini
Untuk menentukan Resultan gaya maka kita bisa melakukan perhitungan matematis seperti di bawah ini
Besar resultan Vektor untuk soal nomor 2 ini adalah
3. Seorang anak berjalan ke utara sejauh 20 meter, kemudian berbelok ke barat sejauh sepuluh meter, dan berbelok lagi ke selatan sejauh 10 meter. Besar perpindahan anak ini adalah ?
Jawab
Untuk menjawab soal ini lebih mudah kita gambarkan perjalanan anak seperti pada gambar di bawah ini.
Seperti terlihat pada gambar perpindahan itu adalah jarak posisi akhir ke posisi awal, pada gambar vektor perpindahannya digambarkan dengan garis AD berwarna merah. Perpindahan itu bisa kita hitung sebagai berikut
Besar perpindahan anak itu adalah
Lain halnya jika yang ditanyakan adalah jarak tempuh anak. Jarak tempuh adalah panjang lintasan yang di tempuh oleh anak maka jarak analah jumlah semua lintasan yang ditempuh anak
Jarak = AB + BC
1. Diketahui dua buah vektor A dan B seperti terlihat pada gambar di bawah ini, besar vektor A 2 N dan besar vektor B 4 N.
Tentukan besar resultan vektor :
a.
b.
c.
Jawab
a. menentukan besar resultan
Untuk menjawab oprasi penjumlahan vektor ini kita harus gambar resultan vektor dengan cara menyatukan pangkal kedua vektor di satu titik seperti pada gambar 1 di bawah ini, resultan R bisa digambarkan dengan metode jajaran genjang seperti pada gambar 1. sudut
adalah sudur antara vektor A dan vektor B |
| Gambar 1 |
Secara umum persamaan untuk menentukan besar resultan 2 buah vektor adalah
 |
| Rumus Resultan Vektor |
Kemudian bisa kita subtitusikan besar vektor dan besar dudut antara kedua vektor kemudian kita hitung
b. Menentukan resultan
Cara pertama
Untuk menghitung resultan pada nomor 1b ini sama seperti 1a tetapi karena vektor B negatif maka rah vektor menjadi kebalikan vektor B apada soal, kemudian kita satukan pangkal vektor A dan Pangkal vektor -B, dan kita bisa menentukan gambar resultan dengan metode jajaran genjang seperti pada gambar 2 di bawah ini.
 |
| Gambar 2 |
vektor, untuk soal 1b besar sudut antara vektor A dan vektor -B adalah .Besar resultan
adalahCara kedua
Cara kedua untuk menentukan besar resultan
adalah dengan menggunakan persamaanBedanya sudut yang kita gunakan menggunakan sudut yang sama seperti pada soal 1a yaitu
.c. Menentukan resultan
Cara Pertama
Untuk menghitung resultan pada nomor 1c ini sama seperti 1a tetapi karena vektor A negatif maka arah vektor menjadi kebalikan vektor A apada soal, kemudian kita satukan pangkal vektor -A dan Pangkal vektor B, dan kita bisa menentukan gambar resultan dengan metode jajaran genjang seperti pada gambar 3 di bawah ini.
 |
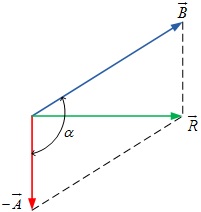| Gambar 3 |
Menghitung resultan vektor soal 1c menggunakan rumus resultan yang sama dengan rumus resultan 1a bedanya terdapat pada sudut antara kedua
vektor, untuk soal 1c besar sudut antara vektor -A dan vektor B adalah .Besar resultan
adalahCara kedua
Cara kedua untuk menentukan besar resultan
adalah dengan menggunakan persamaanBedanya sudut yang kita gunakan menggunakan sudut yang sama seperti pada soal 1a yaitu
.2. Terdapat tiga buah vektor gaya dengan besar vektor gaya pertama adalah 4 N, Besar vektor kedua adalah 6 N, dan besar vektor gaya ketiga adalah 6 N. Arah vektor pertama searah dengan sumbu x positif, arah vektor kedua
terhadap garis sumbu x positif, arah vektor ketiga terhadap arah garis sumbu x negatif seperti pada gambar di bawah ini.Besar resultan ketiga vektor gaya tersebut adalah ?
Jawab
Untuk menjawab persoalan menentukan besar resultan vektor yang berasal dari lebih dari dua vektor kita harus membuat komponen- komponen vektor pada sumbu x dan pada sumbu y untuk vektor-vektor yang tidak searah dengan sumbu x dan sumbu y. Pada soal nomor dua ini terdapat dua buah vektor yang harus dibuat komponennya karena tidak searah dengan sumbu x dan sumbu y yaitu vektor gaya kedua dan vektor gaya ketiga. Komponen-komponen vektor di gambarkan di bawah ini
 |
| Komponen Vektor Gaya 2 |
 |
| Komponen Vektor Gaya 3 |
Gaya pertama tidak perlu dibuat komponen vektornya karena sudah seraah dengan sumbu x positif. Langkah selanjutnya Jumlahkan gaya-gaya yang searah sumbu x, gaya searah sumbu x positif bernilai positif dan gaya yang searah sumbu x negatif bernilai negatif.
Resultan gaya yang searah sumbu x adalah
Jumlahkan gaya-gaya yang searah dengan sumbu y, gaya searah sumbu y positif bernilai positif dan gaya yang searah sumbu y negatif bernilai negatif.
Resultan gaya yang searah sumbu y adalah
Artinya dari tiga vektor yang ada pada persoalan sekarang hanya tinggal 2 vektor seperti pada gambar di bawah ini
Untuk menentukan Resultan gaya maka kita bisa melakukan perhitungan matematis seperti di bawah ini
 |
| Persamaan Untuk Menghitung Resultan 2 Buah Vektor yang Saling Tegak Lurus |
Besar resultan Vektor untuk soal nomor 2 ini adalah
3. Seorang anak berjalan ke utara sejauh 20 meter, kemudian berbelok ke barat sejauh sepuluh meter, dan berbelok lagi ke selatan sejauh 10 meter. Besar perpindahan anak ini adalah ?
Jawab
Untuk menjawab soal ini lebih mudah kita gambarkan perjalanan anak seperti pada gambar di bawah ini.
 |
| Ilustrasi Perjalan Seorang Anak |
Seperti terlihat pada gambar perpindahan itu adalah jarak posisi akhir ke posisi awal, pada gambar vektor perpindahannya digambarkan dengan garis AD berwarna merah. Perpindahan itu bisa kita hitung sebagai berikut
Besar perpindahan anak itu adalah
Lain halnya jika yang ditanyakan adalah jarak tempuh anak. Jarak tempuh adalah panjang lintasan yang di tempuh oleh anak maka jarak analah jumlah semua lintasan yang ditempuh anak
Jarak = AB + BC
Tidak ada komentar:
Posting Komentar