Pada halaman ini akan dibahas mengenai Soal dan Penyelesaian Dua Buah Cermin Lengkung yang Berhadapan. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Soal 1
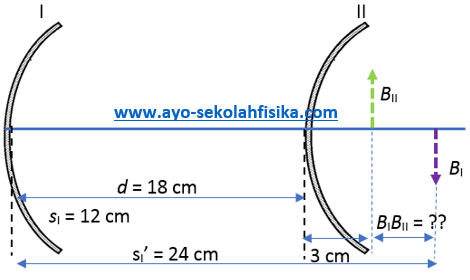
Dua buah cermin diletakkan saling berhadapan dengan sumbu utamanya berimpit. Cermin I adalah cermin cekung dengan jarak fokus 8 cm. Cermin II adalah cermin cembung dengan jari-jari kelengkungan 12 cm. Jarak antara kedua cermin 18 cm. Sebuah benda diletakkan 12 cm di muka cermin I. Hitung jarak antara bayangan pertama yang dibentuk oleh kedua cermin itu.
Jawab:
Untuk cermin I (cermin cekung) jarak fokus, f = +8 cm, jarak benda s = 12 cm, sehingga jarak bayangan adalah
s' = sf/(s – f)
s’ = (12 cm)(8 cm)/(12 cm – 8 cm) = 24 cm
Jadi, bayangan pertama cermin I, BI berada 24 cm di depan cermin I (lihat gambar di atas).
Untuk cermin II (cermin cembung)
Jari-jari R = 12 cm sehingga jarak fokus f = –R/2 = –6 cm.
Dari gambar di bawah, jarak benda ke cermin II, s = 18 cm – 12 cm = 6 cm,
Maka jarak bayangan,
s' = sf/(s – f)
s’ = (6 cm)(6 cm)/[(6 cm) – (–6 cm)] = –3 cm
jadi, bayangan pertama cermin II, BII berada 3 cm di belakang cermin II (lihat gambar di bawah).
Dari gambar di atas diketahui, jarak antara bayangan pertama-kedua cermin (BIBII) adalah
BIBII = 24 cm – 18 cm – 3 cm = 3 cm
Soal 2
Sebuah cermin cekung (Cermin 1) dan sebuah cermin cembung (cermin 2) diletakkan berhadapan pada jarak 55 cm satu sama lain. Kedua cermin mempunyai jejari kelengkungan cermin sama besar 30 cm. Jika sebuah benda diletakkan di antara kedua cermin pada jarak 20 cm dari cermin 1 dan bayangan pertama kali dibentuk oleh cermin 1, maka: (a) Tentukan letak bayangan akhir, (b) jika tinggi benda 2 cm, berapakah tinggi bayangan akhir
Jawab:
(a) Data cermin 1 adalah f1 = R1/2 = 15 cm, s1 = 20 cm, sehingga jarak bayangan oleh cermin 1 dapat ditentukan sebagai berikut,
s1' = s1f/(s1 – f)
s1’ = (20 cm)(15 cm)/(20 cm – 15 cm) = 60 cm
bayangn cermin 1 merupakan benda bagi cermin 2 maka berlaku,
d = s1’ + s2
s2 = 55 cm – 60 cm = –5 cm
karena s2 negatif, berarti benda untuk cermin 2 bersifat maya.
Data cermin cembung (cermin 2) adalah f2 = R2/2 = –15 cm, sehingga bayangan yang dibentuk oleh cermin 2 dapat ditentukan sebagai berikut,
s2' = s2f/(s2 – f)
s2’ = (–5 cm)( –15 cm)/( –5 cm – (–15 cm)) = 7,5 cm (nyata)
jadi, bayangan yang dihasilkan oleh cermin 2 terletak 7,5 cm di depan cermin 2.
(b) Permbesaran total dapat dihitung dengan menggunakan,
M = M1 x M2
M = (–s1’/s1)( –s2’/s2)
= (–60 cm/20 cm)( –7,5 cm/–5 cm)
M = 4,5
Sehingga tinggi bayangan akhir adalah
h' = Mh = (4,5)(2 cm) = 9,0 cm
Soal 3
Cermin cekung dan cembung masing-masing dengan jari-jari 60 cm disusun saling berhadapan dengan sumbu utama berimpit dan jarak pisahnya 100 cm. Suatu benda setinggi 8 cm diletakkan di tengah-tengah di antara kedua cermin. Hitunglah letak dan ukuran bayangan akhir yang terbentuk oleh pemantulan pertama oleh cermin cembung dan kemudian oleh cermin cekung.
Jawab:
Dalam masalah ini, yang pertama memantulkan benda adalah cermin cembung sehingga sebagai cermin 1 adalah cermin cembung dan cermin 2 adalah cermin cekung. Sketsa masalah ditunjukkan oleh gambar.
Jari-jari R1 = R2 = 60 cm
Fokus cermin 1, f1 = –R1/2 = –60 cm/2 = –30 cm (cermin cembung)
Fokus cermin 2, f2 = +R2/2 = +60 cm/2 = +30 cm (cermin cekung)
Pada cermin 1 bayangan yang dihasilkan adalah
s1' = s1f/(s1 – f)
s1’ = (50 cm)( –30 cm)/( 50 cm – (–30 cm)) = –75/4 cm (maya)
bayangan cermin 1 merupakan benda bagi cermin 2, sehingga berlaku
d = s1’ + s2
s2 = 100 cm – (–75/4) cm = 475/4 cm
bayangan pada cermin 2 adalah
s2' = s2f/(s2 – f)
s2’ = (475/4 cm)( 30 cm)/(475/4 cm – 30 cm) = 401 cm (nyata)
Tinggi bayangan akhir kita peroleh dengan menerapkan
M = M1 x M2
M = (–s1’/s1)( –s2’/s2)
= [(–75/4 cm)/50 cm)][401 cm /(475/4))
M = –9/71
Sehingga tinggi bayangan akhir adalah
h' = Mh = (–9/71)(8 cm) = –1 cm
Jadi, bayangan akhir memiliki ukuran tinggi 1,0 cm dan letaknya 401 cm di belakang cermin 2. Tanda negatif pada h2 menyatakan bahwa bayangan akhir adalah terbalik terhadap bendanya semula.
Dua buah cermin diletakkan saling berhadapan dengan sumbu utamanya berimpit. Cermin I adalah cermin cekung dengan jarak fokus 8 cm. Cermin II adalah cermin cembung dengan jari-jari kelengkungan 12 cm. Jarak antara kedua cermin 18 cm. Sebuah benda diletakkan 12 cm di muka cermin I. Hitung jarak antara bayangan pertama yang dibentuk oleh kedua cermin itu.
Jawab:
Untuk cermin I (cermin cekung) jarak fokus, f = +8 cm, jarak benda s = 12 cm, sehingga jarak bayangan adalah
s' = sf/(s – f)
s’ = (12 cm)(8 cm)/(12 cm – 8 cm) = 24 cm
Jadi, bayangan pertama cermin I, BI berada 24 cm di depan cermin I (lihat gambar di atas).
Untuk cermin II (cermin cembung)
Jari-jari R = 12 cm sehingga jarak fokus f = –R/2 = –6 cm.
Dari gambar di bawah, jarak benda ke cermin II, s = 18 cm – 12 cm = 6 cm,
Maka jarak bayangan,
s' = sf/(s – f)
s’ = (6 cm)(6 cm)/[(6 cm) – (–6 cm)] = –3 cm
jadi, bayangan pertama cermin II, BII berada 3 cm di belakang cermin II (lihat gambar di bawah).
Dari gambar di atas diketahui, jarak antara bayangan pertama-kedua cermin (BIBII) adalah
BIBII = 24 cm – 18 cm – 3 cm = 3 cm
Soal 2
Sebuah cermin cekung (Cermin 1) dan sebuah cermin cembung (cermin 2) diletakkan berhadapan pada jarak 55 cm satu sama lain. Kedua cermin mempunyai jejari kelengkungan cermin sama besar 30 cm. Jika sebuah benda diletakkan di antara kedua cermin pada jarak 20 cm dari cermin 1 dan bayangan pertama kali dibentuk oleh cermin 1, maka: (a) Tentukan letak bayangan akhir, (b) jika tinggi benda 2 cm, berapakah tinggi bayangan akhir
Jawab:
(a) Data cermin 1 adalah f1 = R1/2 = 15 cm, s1 = 20 cm, sehingga jarak bayangan oleh cermin 1 dapat ditentukan sebagai berikut,
s1' = s1f/(s1 – f)
s1’ = (20 cm)(15 cm)/(20 cm – 15 cm) = 60 cm
bayangn cermin 1 merupakan benda bagi cermin 2 maka berlaku,
d = s1’ + s2
s2 = 55 cm – 60 cm = –5 cm
karena s2 negatif, berarti benda untuk cermin 2 bersifat maya.
Data cermin cembung (cermin 2) adalah f2 = R2/2 = –15 cm, sehingga bayangan yang dibentuk oleh cermin 2 dapat ditentukan sebagai berikut,
s2' = s2f/(s2 – f)
s2’ = (–5 cm)( –15 cm)/( –5 cm – (–15 cm)) = 7,5 cm (nyata)
jadi, bayangan yang dihasilkan oleh cermin 2 terletak 7,5 cm di depan cermin 2.
(b) Permbesaran total dapat dihitung dengan menggunakan,
M = M1 x M2
M = (–s1’/s1)( –s2’/s2)
= (–60 cm/20 cm)( –7,5 cm/–5 cm)
M = 4,5
Sehingga tinggi bayangan akhir adalah
h' = Mh = (4,5)(2 cm) = 9,0 cm
Soal 3
Cermin cekung dan cembung masing-masing dengan jari-jari 60 cm disusun saling berhadapan dengan sumbu utama berimpit dan jarak pisahnya 100 cm. Suatu benda setinggi 8 cm diletakkan di tengah-tengah di antara kedua cermin. Hitunglah letak dan ukuran bayangan akhir yang terbentuk oleh pemantulan pertama oleh cermin cembung dan kemudian oleh cermin cekung.
Jawab:
Dalam masalah ini, yang pertama memantulkan benda adalah cermin cembung sehingga sebagai cermin 1 adalah cermin cembung dan cermin 2 adalah cermin cekung. Sketsa masalah ditunjukkan oleh gambar.
Jari-jari R1 = R2 = 60 cm
Fokus cermin 1, f1 = –R1/2 = –60 cm/2 = –30 cm (cermin cembung)
Fokus cermin 2, f2 = +R2/2 = +60 cm/2 = +30 cm (cermin cekung)
Pada cermin 1 bayangan yang dihasilkan adalah
s1' = s1f/(s1 – f)
s1’ = (50 cm)( –30 cm)/( 50 cm – (–30 cm)) = –75/4 cm (maya)
bayangan cermin 1 merupakan benda bagi cermin 2, sehingga berlaku
d = s1’ + s2
s2 = 100 cm – (–75/4) cm = 475/4 cm
bayangan pada cermin 2 adalah
s2' = s2f/(s2 – f)
s2’ = (475/4 cm)( 30 cm)/(475/4 cm – 30 cm) = 401 cm (nyata)
Tinggi bayangan akhir kita peroleh dengan menerapkan
M = M1 x M2
M = (–s1’/s1)( –s2’/s2)
= [(–75/4 cm)/50 cm)][401 cm /(475/4))
M = –9/71
Sehingga tinggi bayangan akhir adalah
h' = Mh = (–9/71)(8 cm) = –1 cm
Jadi, bayangan akhir memiliki ukuran tinggi 1,0 cm dan letaknya 401 cm di belakang cermin 2. Tanda negatif pada h2 menyatakan bahwa bayangan akhir adalah terbalik terhadap bendanya semula.


Tidak ada komentar:
Posting Komentar