Pada halaman ini akan dibahas mengenai Soal dan penyelesaian Fluida Dinamis. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Soal 1
Tangki air dengan lubang kebocoran diperlihatkan gambar berikut!

Jarak permukaan fluida ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 1,8 m. Tentukan:
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
Solusi
a) Kecepatan keluarnya air
v = √(2gh)
v = √(2 x 10 x 1,8) = 6 m/s
b) Jarak mendatar terjauh yang dicapai air
X = 2√{h(H-h}
X = 2√{(1,8 (10 – 1,8)} = 3,84 m
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2(H – h)/g)
t = √(2(8,2)/(10)) = 1,28 sekon
Soal 3
Tangki air dengan lubang kebocoran diperlihatkan gambar berikut!

Jarak permukaan fluida ke tanah adalah 10 m dan jarak lubang ke permukaan air adalah 1,8 m. Tentukan:
a) Kecepatan keluarnya air
b) Jarak mendatar terjauh yang dicapai air
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
Solusi
a) Kecepatan keluarnya air
v = √(2gh)
v = √(2 x 10 x 1,8) = 6 m/s
b) Jarak mendatar terjauh yang dicapai air
X = 2√{h(H-h}
X = 2√{(1,8 (10 – 1,8)} = 3,84 m
c) Waktu yang diperlukan bocoran air untuk menyentuh tanah
t = √(2(H – h)/g)
t = √(2(8,2)/(10)) = 1,28 sekon
Soal 2
Soal 2
Posisi pipa besar adalah 6 m diatas tanah dan pipa kecil 1 m diatas tanah. Kecepatan aliran air pada pipa besar adalah 72 km/jam dengan tekanan 25,5 x 105 Pa. Jika perbandingan luas A1 : A2 = 3 : 1, tentukan :
(a) Kecepatan air pada pipa kecil
(b) Selisih tekanan pada kedua pipa
(c) Tekanan pada pipa kecil
(ρair = 1000 kg/m3)

Solusi
h1 = 6 m
h2 = 1 m
v1 = 72 km/jam = 20 m/s
P1 = 5,5 x 105 Pa
A1 : A2 = 3 : 1
a) Kecepatan air pada pipa kecil
Persamaan Kontinuitas :
A1v1 = A2v2
(3)(20) = (1) (v2)
v2 = 60 m/s
b) Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) + ρg(h2 − h1)
P1 − P2 = 1/2(1000)(602 − 202) + (1000)(10)(1 − 6)
P1 − P2 = (500)(3200) − 50000 = 1600000 − 50000
P1 − P2 = 1550000 Pa = 1,55 x 106 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 1,55 x 106
2,55 x 106 − P2 = 1,55 x 106
P2 = 1,0 x 106 Pa
Soal 2
Posisi pipa besar adalah 6 m diatas tanah dan pipa kecil 1 m diatas tanah. Kecepatan aliran air pada pipa besar adalah 72 km/jam dengan tekanan 25,5 x 105 Pa. Jika perbandingan luas A1 : A2 = 3 : 1, tentukan :
(a) Kecepatan air pada pipa kecil
(b) Selisih tekanan pada kedua pipa
(c) Tekanan pada pipa kecil
(ρair = 1000 kg/m3)

Solusi
h1 = 6 m
h2 = 1 m
v1 = 72 km/jam = 20 m/s
P1 = 5,5 x 105 Pa
A1 : A2 = 3 : 1
a) Kecepatan air pada pipa kecil
Persamaan Kontinuitas :
A1v1 = A2v2
(3)(20) = (1) (v2)
v2 = 60 m/s
b) Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) + ρg(h2 − h1)
P1 − P2 = 1/2(1000)(602 − 202) + (1000)(10)(1 − 6)
P1 − P2 = (500)(3200) − 50000 = 1600000 − 50000
P1 − P2 = 1550000 Pa = 1,55 x 106 Pa
c) Tekanan pada pipa kecil
P1 − P2 = 1,55 x 106
2,55 x 106 − P2 = 1,55 x 106
P2 = 1,0 x 106 Pa
Soal 3
Pipa horisontal ditunjukkan pada gambar di bawah ini memiliki area penampang di bagian yang lebih luas 40 cm2 dan pada daerah penyempitan 10 cm2. Air mengalir di pipa dengan debit 6,00 L/s , tentukan: (a) kecepatan air di bagian lebar dan sempit; (b) perbedaan tekanan antara bagian ini; (c) perbedaan ketinggian antara kolom merkuri di manometer. (ρraksa = 13600 kg/m3)
Solusi:
Misalkan kecepatan pada pipa yang besar adalah v1 dan kecepatan pada pipa yang kecil adalah v2, maka A1 = 40 cm2, A2 = 10 cm2, Q = 6,00 L/s = 6,00 x 10-3 m3/s.
(a) Dengan menggunakan konsep kontinuitas, kita peroleh
v1A1 = v2A2 = Q
maka, v1 = Q/A1 = 6,00 x 10-3 m3/(40 x 10-4 m2) = 1,5 m/s
v2 = Q/A2 = 6,00 x 10-3 m3/(10 x 10-4 m2) = 6,0 m/s
(b) Dari Persamaan Bernoulli dan h1 = h2
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) +
P1 − P2 = 1/2(1000)(62 – 1,52)
P1 − P2 = (500)(33,75)
P1 − P2 = 16875 Pa
(c) perbedaan ketinggian kolom raksa adalah
P1 – P2 = ρraksagh
16875 Pa = (13600 kg/m3)(10 m/s2)h
h = 0,124 m = 12,4 cm
Soal 4
Perhatikan gambar!
Jika diameter penampang besar 5 cm dan diameter penampang kecil 3 cm, kecepatan aliran fluida pada pipa kecil v1 = 15 m/s. Tentukan: (a) berapa volume air yang mengalir pada kedua penampang selama 10 menit, (b) besar kecepatan pada penampang besar v2 dan (c) tekanan gauge dalam penampang?
Solusi:
(a) persamaan kontinuitas, A1v1 = A2v2 = Q = V/t
¼ πd12 = V/t
¼ π (0,03 m)2 = (V/600 s)
V = 0,424 m3
(b) dengan menggunakan persamaan kontinuitas, v1A1 = v2A2, karena A1 = ¼ πd2, maka
v1d12 = v2d22
(15 m/s)(3 cm)2 = v2 (5 cm)2
v2 = 5,4 m/s
(c) tekanan gauge adalah perbedaan tekanan dalam pipa horisontal tersebut yaitu,
P1 – P2 = ½ ρ(v12 – v22) = ½ (1000 kg/m3){(15 m/s)2 – (5,4 m/s)2} = 97920 Pa
Soal 5
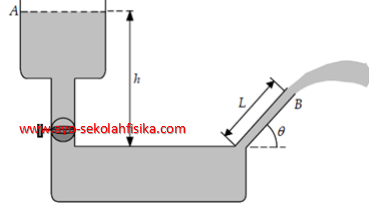
Gambar di bawah ini menunjukkan sebuah tangki air dengan sebuah katup di dasarnya. Jika katup ini dibuka, berapa ketinggian maksimum yang dicapai oleh semburan air yang keluar dari sisi kanan tangki? Anggap h = 10 m, L = 2,0 m, dan θ = 300 dan anggap luas penampang di A jauh lebih besar daripada B.
Misalkan kecepatan pada pipa yang besar adalah v1 dan kecepatan pada pipa yang kecil adalah v2, maka A1 = 40 cm2, A2 = 10 cm2, Q = 6,00 L/s = 6,00 x 10-3 m3/s.
(a) Dengan menggunakan konsep kontinuitas, kita peroleh
v1A1 = v2A2 = Q
maka, v1 = Q/A1 = 6,00 x 10-3 m3/(40 x 10-4 m2) = 1,5 m/s
v2 = Q/A2 = 6,00 x 10-3 m3/(10 x 10-4 m2) = 6,0 m/s
(b) Dari Persamaan Bernoulli dan h1 = h2
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P1 − P2 = 1/2 ρ(v22 − v12) +
P1 − P2 = 1/2(1000)(62 – 1,52)
P1 − P2 = (500)(33,75)
P1 − P2 = 16875 Pa
(c) perbedaan ketinggian kolom raksa adalah
P1 – P2 = ρraksagh
16875 Pa = (13600 kg/m3)(10 m/s2)h
h = 0,124 m = 12,4 cm
Soal 4
Perhatikan gambar!
Jika diameter penampang besar 5 cm dan diameter penampang kecil 3 cm, kecepatan aliran fluida pada pipa kecil v1 = 15 m/s. Tentukan: (a) berapa volume air yang mengalir pada kedua penampang selama 10 menit, (b) besar kecepatan pada penampang besar v2 dan (c) tekanan gauge dalam penampang?
Solusi:
(a) persamaan kontinuitas, A1v1 = A2v2 = Q = V/t
¼ πd12 = V/t
¼ π (0,03 m)2 = (V/600 s)
V = 0,424 m3
(b) dengan menggunakan persamaan kontinuitas, v1A1 = v2A2, karena A1 = ¼ πd2, maka
v1d12 = v2d22
(15 m/s)(3 cm)2 = v2 (5 cm)2
v2 = 5,4 m/s
(c) tekanan gauge adalah perbedaan tekanan dalam pipa horisontal tersebut yaitu,
P1 – P2 = ½ ρ(v12 – v22) = ½ (1000 kg/m3){(15 m/s)2 – (5,4 m/s)2} = 97920 Pa
Soal 5
Gambar di bawah ini menunjukkan sebuah tangki air dengan sebuah katup di dasarnya. Jika katup ini dibuka, berapa ketinggian maksimum yang dicapai oleh semburan air yang keluar dari sisi kanan tangki? Anggap h = 10 m, L = 2,0 m, dan θ = 300 dan anggap luas penampang di A jauh lebih besar daripada B.
Kita terapkan persamaan bernoulli untuk titik A dan B, dengan y = 0 di titik B, dan kecepatan di titik A dita abaikan (mengapa???), maka
PA + ½ ρvA2 + ρgyA = PB + ½ ρvB2 + ρgyB
Karena yB = 0 dan yA = h – L sin θ, maka
PA + ½ ρ(0)2 + ρg(h – L sin θ) = PB + ½ ρvB2 + ρg(0), dan karena PA = PB = tekanan atmosfer maka,
ρg(h – L sin θ) = ½ ρvB2
vB = {2g(h – L sin θ)}1/2 = {2 x 10 m/s2 (10,0 m – 2,00 m x sin 300)} = 13,3 m/s
setelah keluar dari titik B, semburan berbentuk gerak parabola dengan kecepatan awal sebagai
v0y = v0 sin 300 = 13,3 m/s sin 300 = 6,64 m/s, dengan menggunakan hubungan
vy2 = v0y2 + 2gy, maka
(0)2 = (6,64 m/s)2 + 2(-9,8 m/s2)ymaks
Ymaks = 2,25 m.
Soal 6
Sebuah pesawat terbang bergerak dengan kecepatan tertentu sehingga udara yang melalui bagian atas dan bagian bawah sayap yang luas permukaannya 60 m2 bergerak dengan kelajuan masing-masing 320 m/s dan 290 m/s. Berapa besar gaya angkat pada sayap tersebut? (Massa jenis udara 1,3 kg/m3)
Soal 8
PA + ½ ρvA2 + ρgyA = PB + ½ ρvB2 + ρgyB
Karena yB = 0 dan yA = h – L sin θ, maka
PA + ½ ρ(0)2 + ρg(h – L sin θ) = PB + ½ ρvB2 + ρg(0), dan karena PA = PB = tekanan atmosfer maka,
ρg(h – L sin θ) = ½ ρvB2
vB = {2g(h – L sin θ)}1/2 = {2 x 10 m/s2 (10,0 m – 2,00 m x sin 300)} = 13,3 m/s
setelah keluar dari titik B, semburan berbentuk gerak parabola dengan kecepatan awal sebagai
v0y = v0 sin 300 = 13,3 m/s sin 300 = 6,64 m/s, dengan menggunakan hubungan
vy2 = v0y2 + 2gy, maka
(0)2 = (6,64 m/s)2 + 2(-9,8 m/s2)ymaks
Ymaks = 2,25 m.
Soal 6
Sebuah pesawat terbang bergerak dengan kecepatan tertentu sehingga udara yang melalui bagian atas dan bagian bawah sayap yang luas permukaannya 60 m2 bergerak dengan kelajuan masing-masing 320 m/s dan 290 m/s. Berapa besar gaya angkat pada sayap tersebut? (Massa jenis udara 1,3 kg/m3)
Solusi:
v1 = 290 m/s, v2 = 320 m/s, luas sayap A = 60 m2
massa jenis udara ρ = 1,3 kg/m3
sesuai asas Bernoulli, kita dapat menentukan beda tekanan bagian atas dan bagian bawah sayap
p1 – p2 = ½ ρ(v22 – v12)
gaya angkat yang dihasilkan sayap sama dengan hasil kali beda tekanan (p1 – p2) dan luas permukaan sayap (A)
F1 – F2 = (p1 – p2)A
F1 – F2 = ½ ρA(v22 – v12) = ½ (1,3 kg/m3)(60 m2)((320 m/s)2 – (290 m/s)2)
F1 – F2 = 713 700 N
Jadi, besarnya gaya angkat sayap adalah 713 700 N
Soal 7

Air mengalir ke bawah melalui suatu pipa seperi pada gambar dengan laju alir 15 L/s. Jika air memasuki ujung pipa 2 dengan kelajuan 5,0 m/s, berapa beda tekanan di antara kedua ujung pipa tersebut, jika h = 1,5 m dan luas penampang pipa besar A1 = 10 cm2.
Solusi:
h2 = 6 m
h1 = 0
v2 = 5 m/s
A1 = 10 cm2
Q = 15 L/s = 1,5 x 10-2 m3/s
maka Q = v2A2 à A2 = (1,5 x 10-2 m3/s)/(5,0 m/s) = 0,3 x 10-2 m2 = 30 cm2
dan Q = v1A1 à v1 = (1,5 x 10-2 m3/s)/(0,1 x 10-2 m2) = 15 m/s
Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P2 – P1 = 1/2 ρ(v12 − v12) + ρg(h1 – h2)
P2 − P1 = 1/2(1000)(252 − 52) + (1000)(10)(0 – 1,5)
P2 – P1 = (500)(600) – 15000 = 300000 − 15000
P2 – P1 = 285000 Pa = 285 kPa
v1 = 290 m/s, v2 = 320 m/s, luas sayap A = 60 m2
massa jenis udara ρ = 1,3 kg/m3
sesuai asas Bernoulli, kita dapat menentukan beda tekanan bagian atas dan bagian bawah sayap
p1 – p2 = ½ ρ(v22 – v12)
gaya angkat yang dihasilkan sayap sama dengan hasil kali beda tekanan (p1 – p2) dan luas permukaan sayap (A)
F1 – F2 = (p1 – p2)A
F1 – F2 = ½ ρA(v22 – v12) = ½ (1,3 kg/m3)(60 m2)((320 m/s)2 – (290 m/s)2)
F1 – F2 = 713 700 N
Jadi, besarnya gaya angkat sayap adalah 713 700 N
Soal 7

Air mengalir ke bawah melalui suatu pipa seperi pada gambar dengan laju alir 15 L/s. Jika air memasuki ujung pipa 2 dengan kelajuan 5,0 m/s, berapa beda tekanan di antara kedua ujung pipa tersebut, jika h = 1,5 m dan luas penampang pipa besar A1 = 10 cm2.
Solusi:
h2 = 6 m
h1 = 0
v2 = 5 m/s
A1 = 10 cm2
Q = 15 L/s = 1,5 x 10-2 m3/s
maka Q = v2A2 à A2 = (1,5 x 10-2 m3/s)/(5,0 m/s) = 0,3 x 10-2 m2 = 30 cm2
dan Q = v1A1 à v1 = (1,5 x 10-2 m3/s)/(0,1 x 10-2 m2) = 15 m/s
Selisih tekanan pada kedua pipa
Dari Persamaan Bernoulli :
P1 + 1/2 ρv12 + ρgh1 = P2 + 1/2 ρv22 + ρgh2
P2 – P1 = 1/2 ρ(v12 − v12) + ρg(h1 – h2)
P2 − P1 = 1/2(1000)(252 − 52) + (1000)(10)(0 – 1,5)
P2 – P1 = (500)(600) – 15000 = 300000 − 15000
P2 – P1 = 285000 Pa = 285 kPa
Soal 8
Sebuah venturimeter tanpa manometer diperlihatkan pada gambar digunakan untuk mengukur kecepatan air. Perbandingan luas penmpang 1 dan penampang 2 adalah 5 : 3, Jika ketinggian masing-masing pipa h1 = 9 cm dan h2 = 4 cm. Tentukan: (a) Perbendaan tekanan antara penampang 1 dan penampang 2 dan (b) kecepatan air pada penampang 1 dan penampang 2!
Solusi:
(a) Tekanan pada penampang besar dan penampang kecil diperoleh dengan persamaan p = ρgh, maka
p1 = ρgh1 = (1000 kg/m3)(10 m/s2)(0,09 m) = 900 Pa
p2 = ρgh2 = (1000 kg/m3)(10 m/s2)(0,04 m) = 400 Pa
maka p1 – p2 = 500 Pa
(b) Aliran air pada pipa horisontal berlaku persamaan Bernoulli yaitu
p1 + ½ ρv12 + ρgy1 = p2 + ½ ρv22 + ρgy2 à y1 = y2, maka
p1 – p2 = ½ ρ(v22 – v12)
500 Pa = ½ (1000 kg/m3)(v22 – v12)
(v22 – v12) = 1 m2/s2
Persamaan kontinuitas memberikan A1v1 = A2v2 à v1/v2 = 3/5 à v1 = (3/5)v2, sehingga
v22 – [(3/5)v2]2 = 1 m2/s2
(16/25)v22 = 1 m2/s2
v2 = 1,25 m/s
dan v1 = 0,75 m/s
Soal 9
Sebuah pipa pancur memiliki mulut pipa 2 cm. Pancuran didesain untuk dapat memancarkan air secara vertikal ke atas setinggi 20 m dari permukaan tanah. Pipa pancur dihubungkan ke permukaan air yang terletak 5 m di bawah tanah. Bila diameter mulut pompa 4 cm. Berapakah tekanan pompa harus didesain?
Jawab:
pipa yang lebih lebar (indeks 1) dan pipa yang kecil (indeks 2), berlaku hukum kontinuitas,
v1A1 = v2A2
v1d12 = v2d22, maka
v1/v2 = (d2/d1)2 = (2/4)2 = ¼
v2 = 4v1
air keluar dari pipa sempit (d2) dengan kecepatan v2 dan semburan naik setinggi 20 m, maka berlaku
½ mv22 = mgh
½ v22 = 10 kg/m2 x 20 m
v2 = 20 m/s, maka
v1 = v2/4 = 5 m/s
Sehingga dengan menggunakan persamaan Bernoulli kita peroleh,
P1 + ½ρv12 + ρgh1 = P2 + ½ρv22 + ρgh2
Ppompa + ½ (1000 kg/m3)(5 m/s)2 + 0 = 100 kPa + ½ (1000 kg/m3)(20 m/s)2 + (1000 kg/m3)(10 m/s2)(5 m)
Ppompa + 12,5 kPa = 100 kPa + 200 kPa + 50 kPa
Ppompa = 337,5 kPa
Jadi, agar air dapat keluar dari pancuran setinggi 20 m maka pompa yang dipakai minimal menghasilkan tekanan sebesar 337,5 kPa.
Solusi:
(a) Tekanan pada penampang besar dan penampang kecil diperoleh dengan persamaan p = ρgh, maka
p1 = ρgh1 = (1000 kg/m3)(10 m/s2)(0,09 m) = 900 Pa
p2 = ρgh2 = (1000 kg/m3)(10 m/s2)(0,04 m) = 400 Pa
maka p1 – p2 = 500 Pa
(b) Aliran air pada pipa horisontal berlaku persamaan Bernoulli yaitu
p1 + ½ ρv12 + ρgy1 = p2 + ½ ρv22 + ρgy2 à y1 = y2, maka
p1 – p2 = ½ ρ(v22 – v12)
500 Pa = ½ (1000 kg/m3)(v22 – v12)
(v22 – v12) = 1 m2/s2
Persamaan kontinuitas memberikan A1v1 = A2v2 à v1/v2 = 3/5 à v1 = (3/5)v2, sehingga
v22 – [(3/5)v2]2 = 1 m2/s2
(16/25)v22 = 1 m2/s2
v2 = 1,25 m/s
dan v1 = 0,75 m/s
Soal 9
Sebuah pipa pancur memiliki mulut pipa 2 cm. Pancuran didesain untuk dapat memancarkan air secara vertikal ke atas setinggi 20 m dari permukaan tanah. Pipa pancur dihubungkan ke permukaan air yang terletak 5 m di bawah tanah. Bila diameter mulut pompa 4 cm. Berapakah tekanan pompa harus didesain?
Jawab:
pipa yang lebih lebar (indeks 1) dan pipa yang kecil (indeks 2), berlaku hukum kontinuitas,
v1A1 = v2A2
v1d12 = v2d22, maka
v1/v2 = (d2/d1)2 = (2/4)2 = ¼
v2 = 4v1
air keluar dari pipa sempit (d2) dengan kecepatan v2 dan semburan naik setinggi 20 m, maka berlaku
½ mv22 = mgh
½ v22 = 10 kg/m2 x 20 m
v2 = 20 m/s, maka
v1 = v2/4 = 5 m/s
Sehingga dengan menggunakan persamaan Bernoulli kita peroleh,
P1 + ½ρv12 + ρgh1 = P2 + ½ρv22 + ρgh2
Ppompa + ½ (1000 kg/m3)(5 m/s)2 + 0 = 100 kPa + ½ (1000 kg/m3)(20 m/s)2 + (1000 kg/m3)(10 m/s2)(5 m)
Ppompa + 12,5 kPa = 100 kPa + 200 kPa + 50 kPa
Ppompa = 337,5 kPa
Jadi, agar air dapat keluar dari pancuran setinggi 20 m maka pompa yang dipakai minimal menghasilkan tekanan sebesar 337,5 kPa.





Tidak ada komentar:
Posting Komentar