Pada halaman ini akan dibahas mengenai Soal dan penyelesaian Gerak Harmonik sederhana. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Soal 1
Suatu benda berosilasi dengan Gerak Harmonik sederhana sepanjang sumbu y. Seiring waktu posisinya berubah-ubah sesuai persamaan
Solusi:
Persamaan GHS, y = (4,00 cm) cos (2πt + π/4), maka
(a) Amplitudo, A = 4,00 cm
(b) Kecepatan ghs, vy = dy/dt = (4,00 cm x 2π) [- sin (2πt + π/4)] = – 8π sin (2πt + π/4) cm/s
Percepatan ghs, ay = d2y/dt2 = dvy/dt = (– 8π x 2π) cos (2πt + π/4) = – 16π2 cos (2πt + π/4) cm/s2
(c) Pada t = 1/8 dtk,
⇒ vy = – 8π sin (2πt + π/4) cm/s = – 8π sin [2π x (1/8) + π/4] cm/s = – 8π cm/s
⇒ay = – 16π2 cos (2πt + π/4) = – 16π2 cos [2π x (1/8) + π/4] cm/s2 = 0
(d)Kelajuan maksimum dan kecepatan maksimumnya adalah (lihat b)
vmaks = – 8π cm/s dan amaks = – 16π2 cm/s2
(e) Pada t = 0, y = (4,00 cm) cos (2π x 0 + π/4) = 4,00 cm
Pada t = 1/8 s, y = (4,00 cm) cos (2πt + π/4) = (4,00 cm )sin [2π x (1/8) + π/4] cm = 0
Soal 2
Solusi
(a) Persamaan simpangan adalah x = A sin θ dengan θ = ωt + θ0. Simpangan = setengah amplitudo, artinya
x = A sin θ = ½ A
sin θ = ½ dan θ = π/6
karena tidak diketahui, maka anggap sudut fase awal θ0 = 0, maka
θ = ωt = π/6
(2π/T) = π/6
t = (π/6)(T/2π) = T/12
(b) kecepatan adalah turunan pertama dari fungsi posisi. Karena posisi x = A sin (ωt + θ0), maka
v = dx/dt = Aω cos (ωt + θ0)
dengan vmaks = ωA
diberikan v = vmaks/2, maka
Aω cos (ωt + θ0) = ωA/2
cos (ωt + θ0) = ½
dari rumus trigonometri sin2x + cos2x = 1, maka
Jadi simpangan x adalah
Soal 3
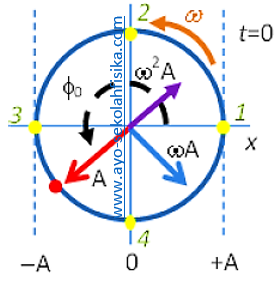
Diagram di bawah menunjukkan gerakan massa 2,00 kg pada pegas horizontal. (a) Menggambar lingkaran referensi. (b) Cari fase konstan, (c) Tuliskan persamaan perpindahan sebagai fungsi waktu, (d) berapa konstanta pegas? (e) Berapa totalnya energi? (f) Berapa kecepatan maksimum? (g) Berapakah percepatan maksimum? (h) Kapan tepatnya massa berada di titik setimbang dan bergerak ke kanan? (i) Kapan tepatnya massa akan berada di titik C?
Solusi:
Memeriksa grafik kita melihat bahwa perpindahan terbesar adalah 10 cm, sehingga A = 0,10 m. Kita juga melihat bahwa gerakan berulang setiap 0,2 detik, sehingga T = 0,2 s. frekuensi sudut berkaitan dengan periode dengan ω = 2π/T, sehingga ω = 10π rad/s.
(a) Pada t = 0, kita dapat membaca dari sisi grafik yaitu x = 7,5 cm = 0,075 m. Posisi negatif X menempatkan benda di baik kuadran II atau III dari lingkaran. Untuk menentukan kuadran yang benar, perhatikan bahwa pada saat t meningkat kurva melewati titik nol (titik seimbang), diberi label titik A pada diagram, dan itu bergerak dari negatif ke posisi positif sehingga pindah ke kanan. Ini adalah perilaku partikel pada kuadran III, sehingga lingkaran referensi terlihat seperti di bawah ini
(b) Kita bisa mengambil persamaan umum, x = Acos (ωt + φ0) dan mengganti t = 0 untuk menemukan φ0, yaitu- 0,075 = 0,10 cos (0 + φ0)cos φ0 = – 0,075φ0 = cos-1(-0,075)Pemecahan hasil φ0 = 138,6 ° (2,419 rad) atau φ0 = 221,4 ° (3,864 rad). Jawaban kedua adalah di kuadran ketiga dan dengan demikian φ0 = 221,4 ° (3,864 rad)
(c) persamaan perpindahan sebagai fungsi waktu adalah sebagai x = Acos (ωt + φ0) = (0,10 m) cos (10πt + 3,864)
(d) konstanta pegas, ω2 = k/m, maka k = mω2 = (2 kg)(10π rad/s) = 1974 N/m
(e) energi total ghs adalah E = ½ kA2 = ½ (1974 N/m)(0,1 m)2 = 9,870 J
(f) kecepatan maksimum, vmaks = ωA = (10π rad/s)(0,1 m) = π m/s
(g) percepatan maksimum, amaks = -ω2A = -(10π rad/s)2(0,1 m) = 9870 m/s2
(h) Untuk menentukan ketika benda bergerak ke kanan pada kesetimbangan (berlabel A di xt diberikan grafik), ditunjuk pada titik 3 pada lingkaran referensi yang diberikan di atas. Jadi benda memutar 270 ° dari 221,4 °. Sejak berputar 360 ° mengambil satu periode yang di sini adalah 0,2 s, tA = 48,6 / 360 × 0,2 s = 0,027 s.
(i) Titik C dalam diagram terjadi pada titik 1 pada lingkaran referensi tetapi perhatikan bahwa titik C lebih dari satu periode T dari t = 0. Kita perlu menghitung waktu untuk memutar ke titik 1 tapi kemudian menambahkan satu periode. Sudut memutar melalui 360 ° – 221,4 ° = 138,6 °. Jadi tC = 138,6/360 × 0,2 s + 0,2 s = 0,277 s.
Soal 4
Dua persamaan GHS yaitu x = a sin (ωt – α) dan y = b cos (ωt – α). Tentukan beda fase antara keduanya!
Soal 7
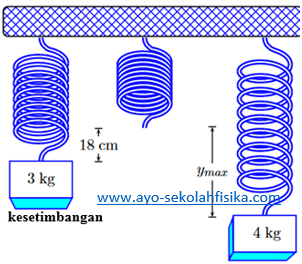
Sebuah balok massa 3 kg digantung pada sebuah pegas dan menyebabkan pegas meregang 18 cm pada kesetimbangan, seperti ditunjukkan di bawah. Balok 3 kg kemudian diganti dengan 4 kg, dan balok baru dilepaskan dari posisi yang ditunjukkan di bawah, di mana pegas meregang. Seberapa jauh akan balok 4 kg jatuh sebelum akan berbalik arah? Untuk kasus balok baru, jarak total jatuh dua kali amplitudo osilasi. Percepatan gravitasi adalah 9,8 m /s2.
Solusi:
Diketahui m1 = 3 kg, m2 = 4 kg, y1 = 18 cm, dengan menerapkan hukum Hook, F = kx, maka
F1/F2 = m1g/m2g = ky1/ky2
y2 = m2y1/m1 = (4 kg)(18 cm)/3 kg = 24 cm
karena amplitudo adalah setengah dari gerak vertikal maka
ymaks = 2y2 = 2 x 24 cm = 48 cm
Soal 8
Soal 11: Sebuah partikel melakukan dua gerakan harmonis sederhana dalam arah yang sama memiliki amplitudo yang sama A dan frekuensi yang sama, f. Jika amplitudo resultan sama dengan A, Tentukan perbedaan fase antara gerakan harmonik itu?
Solusi: misalkan perbedaan fasa antara kedua gerakan itu adalah ф.Kedua gerakan yang sepanjang arah yang sama, sehingga x = x1 + x2
Suatu benda berosilasi dengan Gerak Harmonik sederhana sepanjang sumbu y. Seiring waktu posisinya berubah-ubah sesuai persamaan
y = (4,00 cm) cos (2πt + π/4)
di mana t dalam detik dan sudut-sudutnya menggunakan satuan radian. (a) Tentukan amplitudo, kecepatan sudut, frekuensi dan priode geraknya, (b) Hitung kecepatan dan percepatan benda pada saat t, (c) Tentukan kecepatan dan percepatan benda pada saat t = 1/8 s, (d) Tentukan kelajuan maksimum dan percepatan maksimumnya dan (e) Tentukan posisi benda antara t = 0 dan t = 1/8 sSolusi:
Persamaan GHS, y = (4,00 cm) cos (2πt + π/4), maka
(a) Amplitudo, A = 4,00 cm
(b) Kecepatan ghs, vy = dy/dt = (4,00 cm x 2π) [- sin (2πt + π/4)] = – 8π sin (2πt + π/4) cm/s
Percepatan ghs, ay = d2y/dt2 = dvy/dt = (– 8π x 2π) cos (2πt + π/4) = – 16π2 cos (2πt + π/4) cm/s2
(c) Pada t = 1/8 dtk,
⇒ vy = – 8π sin (2πt + π/4) cm/s = – 8π sin [2π x (1/8) + π/4] cm/s = – 8π cm/s
⇒ay = – 16π2 cos (2πt + π/4) = – 16π2 cos [2π x (1/8) + π/4] cm/s2 = 0
(d)Kelajuan maksimum dan kecepatan maksimumnya adalah (lihat b)
vmaks = – 8π cm/s dan amaks = – 16π2 cm/s2
(e) Pada t = 0, y = (4,00 cm) cos (2π x 0 + π/4) = 4,00 cm
Pada t = 1/8 s, y = (4,00 cm) cos (2πt + π/4) = (4,00 cm )sin [2π x (1/8) + π/4] cm = 0
Soal 2
Sebuah benda menempuh gerak harmonik sederhana dengan amplitudo A dan periode T. (a) berapakah waktu minimum yang diperlukan benda agar simpangannya sama dengan setengah amplitudonya?, (b) berapakah simpangannya ketika kecepatannya setengah dari kecepatan maksimumnya?
Solusi
(a) Persamaan simpangan adalah x = A sin θ dengan θ = ωt + θ0. Simpangan = setengah amplitudo, artinya
x = A sin θ = ½ A
sin θ = ½ dan θ = π/6
karena tidak diketahui, maka anggap sudut fase awal θ0 = 0, maka
θ = ωt = π/6
(2π/T) = π/6
t = (π/6)(T/2π) = T/12
(b) kecepatan adalah turunan pertama dari fungsi posisi. Karena posisi x = A sin (ωt + θ0), maka
v = dx/dt = Aω cos (ωt + θ0)
dengan vmaks = ωA
diberikan v = vmaks/2, maka
Aω cos (ωt + θ0) = ωA/2
cos (ωt + θ0) = ½
dari rumus trigonometri sin2x + cos2x = 1, maka
Jadi simpangan x adalah
Soal 3
Solusi:
Memeriksa grafik kita melihat bahwa perpindahan terbesar adalah 10 cm, sehingga A = 0,10 m. Kita juga melihat bahwa gerakan berulang setiap 0,2 detik, sehingga T = 0,2 s. frekuensi sudut berkaitan dengan periode dengan ω = 2π/T, sehingga ω = 10π rad/s.
(a) Pada t = 0, kita dapat membaca dari sisi grafik yaitu x = 7,5 cm = 0,075 m. Posisi negatif X menempatkan benda di baik kuadran II atau III dari lingkaran. Untuk menentukan kuadran yang benar, perhatikan bahwa pada saat t meningkat kurva melewati titik nol (titik seimbang), diberi label titik A pada diagram, dan itu bergerak dari negatif ke posisi positif sehingga pindah ke kanan. Ini adalah perilaku partikel pada kuadran III, sehingga lingkaran referensi terlihat seperti di bawah ini
(c) persamaan perpindahan sebagai fungsi waktu adalah sebagai x = Acos (ωt + φ0) = (0,10 m) cos (10πt + 3,864)
(d) konstanta pegas, ω2 = k/m, maka k = mω2 = (2 kg)(10π rad/s) = 1974 N/m
(e) energi total ghs adalah E = ½ kA2 = ½ (1974 N/m)(0,1 m)2 = 9,870 J
(f) kecepatan maksimum, vmaks = ωA = (10π rad/s)(0,1 m) = π m/s
(g) percepatan maksimum, amaks = -ω2A = -(10π rad/s)2(0,1 m) = 9870 m/s2
(h) Untuk menentukan ketika benda bergerak ke kanan pada kesetimbangan (berlabel A di xt diberikan grafik), ditunjuk pada titik 3 pada lingkaran referensi yang diberikan di atas. Jadi benda memutar 270 ° dari 221,4 °. Sejak berputar 360 ° mengambil satu periode yang di sini adalah 0,2 s, tA = 48,6 / 360 × 0,2 s = 0,027 s.
(i) Titik C dalam diagram terjadi pada titik 1 pada lingkaran referensi tetapi perhatikan bahwa titik C lebih dari satu periode T dari t = 0. Kita perlu menghitung waktu untuk memutar ke titik 1 tapi kemudian menambahkan satu periode. Sudut memutar melalui 360 ° – 221,4 ° = 138,6 °. Jadi tC = 138,6/360 × 0,2 s + 0,2 s = 0,277 s.
Soal 4
Dua persamaan GHS yaitu x = a sin (ωt – α) dan y = b cos (ωt – α). Tentukan beda fase antara keduanya!
Solusi:
x = a sin (ωt – α) dan y = b cos (ωt – α) = b sin (ωt – α + π/2),
maka beda fase antara keduanya adalah (ωt – α + π/2) – ((ωt – α ) = 900
Soal 5
Dua partikel melakukan GHS dengan amplitudo dan frekuensi yang sama di sepanjang garis lurus yang sama. Keduanya melewati satu lagi ketika akan di arah yang berlawanan. Setiap kali perpindahan keduanya adalah setengah dari amplitudo. Tentukan perbedaan fasa antara kedua partikel.
Solusi:
Misalnya simpangan kedua partikel adalah y = A sin ωt dan y = A sin (ωt + φ)
Kasus pertama, A/2 = A sin ωt à sin ωt = ½, jadi cos ωt = √3/2,
Kasus kedua, A/2 = A sin (ωt + φ) à ½ = [sin ωt cos φ + cos ωt sin φ]
⇒½ = [½ cos φ + (√3/2) sin φ]
⇒1 = cos φ + √3 sin φà 1 – cos φ = √3 sin φ
⇒(1 – cos φ)2 = (√3 sin φ)2 = 3(1 – cos2φ)
⇒Maka cos φ = + 1 atau cos φ = – ½
Jadi φ = 00 atau φ = 1200
Soal 6
Perpindahan sebuah partikel yang sedang bergerak harmonik sederhanan diberikan oleh x = 5 sin 2t, dengan x dalam sentimeter dan t dalam sekon. Jika periode gerakan adalah T, tentukan percepatan partikel pada t = T/6 s!
Solusi:
Persamaan posisi partikel adalah x = 5 sin 2t = A sin ωt, maka ω = 2 rad/s = 2π/T, maka T = π s. Dengan menggunakan diferensial tingkat dua kita peroleh persamaan percepatan
a = d2x/dt2 = – 20 sin 2t
pada saat t = T/6 s = π/6 s, percepatan partikel adalah
a = – 20 sin 2(π/6) = -20 sin π/3 = -10√3 m/s2
x = a sin (ωt – α) dan y = b cos (ωt – α) = b sin (ωt – α + π/2),
maka beda fase antara keduanya adalah (ωt – α + π/2) – ((ωt – α ) = 900
Soal 5
Dua partikel melakukan GHS dengan amplitudo dan frekuensi yang sama di sepanjang garis lurus yang sama. Keduanya melewati satu lagi ketika akan di arah yang berlawanan. Setiap kali perpindahan keduanya adalah setengah dari amplitudo. Tentukan perbedaan fasa antara kedua partikel.
Solusi:
Misalnya simpangan kedua partikel adalah y = A sin ωt dan y = A sin (ωt + φ)
Kasus pertama, A/2 = A sin ωt à sin ωt = ½, jadi cos ωt = √3/2,
Kasus kedua, A/2 = A sin (ωt + φ) à ½ = [sin ωt cos φ + cos ωt sin φ]
⇒½ = [½ cos φ + (√3/2) sin φ]
⇒1 = cos φ + √3 sin φà 1 – cos φ = √3 sin φ
⇒(1 – cos φ)2 = (√3 sin φ)2 = 3(1 – cos2φ)
⇒Maka cos φ = + 1 atau cos φ = – ½
Jadi φ = 00 atau φ = 1200
Soal 6
Perpindahan sebuah partikel yang sedang bergerak harmonik sederhanan diberikan oleh x = 5 sin 2t, dengan x dalam sentimeter dan t dalam sekon. Jika periode gerakan adalah T, tentukan percepatan partikel pada t = T/6 s!
Solusi:
Persamaan posisi partikel adalah x = 5 sin 2t = A sin ωt, maka ω = 2 rad/s = 2π/T, maka T = π s. Dengan menggunakan diferensial tingkat dua kita peroleh persamaan percepatan
a = d2x/dt2 = – 20 sin 2t
pada saat t = T/6 s = π/6 s, percepatan partikel adalah
a = – 20 sin 2(π/6) = -20 sin π/3 = -10√3 m/s2
Soal 7
Sebuah balok massa 3 kg digantung pada sebuah pegas dan menyebabkan pegas meregang 18 cm pada kesetimbangan, seperti ditunjukkan di bawah. Balok 3 kg kemudian diganti dengan 4 kg, dan balok baru dilepaskan dari posisi yang ditunjukkan di bawah, di mana pegas meregang. Seberapa jauh akan balok 4 kg jatuh sebelum akan berbalik arah? Untuk kasus balok baru, jarak total jatuh dua kali amplitudo osilasi. Percepatan gravitasi adalah 9,8 m /s2.
Solusi:
Diketahui m1 = 3 kg, m2 = 4 kg, y1 = 18 cm, dengan menerapkan hukum Hook, F = kx, maka
F1/F2 = m1g/m2g = ky1/ky2
y2 = m2y1/m1 = (4 kg)(18 cm)/3 kg = 24 cm
karena amplitudo adalah setengah dari gerak vertikal maka
ymaks = 2y2 = 2 x 24 cm = 48 cm
Soal 8
Sebuah partikel yang melakukan GHS berada pada posisi dan gerak ke arah seperti ditunjukkan pada gambar. Jika amplitudo dan frekuensi ghs adalah 4 cm dan 2 Hz, maka tentukan posisi partikel setelah t = 1 detik dan ke arah kanan atau ke kiri?
Solusi:
Diketahui, f = 2 Hz, A = 4 cm, ω =2πf = 4π rad/s.
Kita bisa mengambil persamaan umum, x = A cos (ωt + φ0) dan mengganti t = 0 untuk menemukan φ0, yaitu
2 cm = 4 cm cos (0 + φ0)
cos φ0 = ½
φ0 = cos-1(1/2) = π/3 atau φ0 = 5π/3
Pemecahan hasil φ0 = 60° (= π/3 rad) atau φ0 = 300° (= 5π/3 rad)
Jawaban pertama adalah di kuadran kesatu dan dengan demikian φ0 = 60° (= π/3 rad) karena awalnya partikel bergerak ke kiri yaitu dari kuadran I ke kuadran II. Sehingga persamaan perpindahan sebagai fungsi waktu adalah sebagai
x = A cos (ωt + φ0) = (4 cm) cos (4πt + π/3)
maka pada saat t = 1 detik,
x = (4 cm) cos (4πt + π/3)
x = (4 cm) cos (4π x 1 + π/3)
x = (4 cm) cos (13π/3) = 2 cm ke kiri
Soal 9: Sebuah blok kecil berosilasi bolak-balik pada permukaan cekung halus dengan jari-jari R = 2,45 m (Lihat gambar). Cari periode osilasi tersebut. Jika g = 9,8 m /s2. 
Diketahui, f = 2 Hz, A = 4 cm, ω =2πf = 4π rad/s.
Kita bisa mengambil persamaan umum, x = A cos (ωt + φ0) dan mengganti t = 0 untuk menemukan φ0, yaitu
2 cm = 4 cm cos (0 + φ0)
cos φ0 = ½
φ0 = cos-1(1/2) = π/3 atau φ0 = 5π/3
Pemecahan hasil φ0 = 60° (= π/3 rad) atau φ0 = 300° (= 5π/3 rad)
Jawaban pertama adalah di kuadran kesatu dan dengan demikian φ0 = 60° (= π/3 rad) karena awalnya partikel bergerak ke kiri yaitu dari kuadran I ke kuadran II. Sehingga persamaan perpindahan sebagai fungsi waktu adalah sebagai
x = A cos (ωt + φ0) = (4 cm) cos (4πt + π/3)
maka pada saat t = 1 detik,
x = (4 cm) cos (4πt + π/3)
x = (4 cm) cos (4π x 1 + π/3)
x = (4 cm) cos (13π/3) = 2 cm ke kiri
Soal 9: Sebuah blok kecil berosilasi bolak-balik pada permukaan cekung halus dengan jari-jari R = 2,45 m (Lihat gambar). Cari periode osilasi tersebut. Jika g = 9,8 m /s2. Solusi: Biarkan balok berada di sudut ‘θ’ dengan vertikal dan dilepaskan sehingga mengalami gerakan bolak-balik. Gaya yang bekerja pada balok ditunjukkan pada gambar di bawah ini!
Gaya yang mempercepat balok menuju posisi dasar permukaan adalah, F = mgsinθ
Karena θ sangat kecil maka, sinθ ≈ θ, oleh karena itu, F = – mgθ atau a = -gθ
Jika x merupakan perpindahan balok dari posisi mendatar maka, θ = x/R
Sehingga percepatan balok menjadi
Jika suatu partikel mengalami gerak harmonik sederhana, percepatan yang dialami partikel tersebut adalah
Maka Sekarang dua persamaan untuk ‘a’, kita mendapatkan Oleh karena ω = 2п/ T, maka periode osilasi balok tersebut adalah
Sehingga dari data: R = 2,45 m dan g = 9,8 m/s2, kita peroleh perode osilasi balok tersebut adalah π sekon!
Solusi: misalkan perbedaan fasa antara kedua gerakan itu adalah ф.Kedua gerakan yang sepanjang arah yang sama, sehingga x = x1 + x2
oleh karena itu
sehingga,
atau
di mana amplitudo gerakan yang dihasilkan adalah
Nilai amplitudo ini yang sama dengan A untuk masalah yang diberikan. Oleh karena itu,
atau
karena
maka
Tidak ada komentar:
Posting Komentar