Pada halaman ini akan dibahas mengenai Soal Fluida Statis dan penyelesaiannya. Semua informasi ini kami rangkum dari berbagai sumber. Semoga memberikan faedah bagi kita semua.
Soal 1: Seorang gadis bermassa 50 kg menggunakan sepatu high heel. Diameter ujung bawah tumit sepatu 1.0 cm. Tentukan tekanan yang diberikan tumit pada lantai?Jawab
Massa gadis, m = 50 kg
Diameter tumit sepatu, d = 1 cm = 0.01 m
Radius tumit sepatu, r = d/2 = 0.005 m
Luas alas tumit sepatu = πr2
= π (0.005)2
= 7.85 × 10–5 m2
gaya yang diberikan oleh tumit pada lantai adalah:
F = mg
= 50 × 9.8
= 490 N
tekanan oleh tumit pada lantai adalah:
P = gaya /luas = 490 / (7.85 × 10-5) = 6.24 × 106 Nm-2
maka tekanan yang berikan tumit pada lantai adalah sebesar 6.24 × 106 Nm–2.
Soal 2: Pada gambar di bawah ini, gambar (a) menunjukkan selaput cairan tipis menopang benda seberat 0,045 N. Berapakah berat benda yang didukung oleh selaput cairan yang sama pada suhu yang sama untuk gambar (b) dan (c)! Jelaskan jawaban anda!!
Jawab:
Pada kasus (a): Panjang selaput cairan yang di dukung berat adalah, l = 40 cm = 0.4 cm
berat yang tergantung ada cairan adalah, W = 4.5 × 10–2 N
Sebuah selaput cairang memiliki dua permukaan bebas.
∴ tegangan permukaan = W /2l
= 4.5 × 10-2 / (2 × 0.4) = 5.625 × 10-2 N/m
Pada kasus (b) dan (c) karena cairan sama dan pada suhu yang sama maka tegangan permukaannya juga sama yaitu 5.625 × 10-2 N/m.
Karena panjang selaput pada setiap kasus sama maka berat yang didukung selaput untuk setiap kasus adalah sama yaitu W = 4.5 × 10–2 N.
Soal 3: Merkurius memiliki sudut kontak sama dengan 140 ° dengan kaca soda kapur. Sebuah tabung sempit radius 1,00 mm terbuat dari kaca ini dicelupkan ke dalam palung yang mengandung merkuri. Berapa besar merkuri turun dalam tabung relatif terhadap permukaan cairan luar? tegangan permukaan air raksa pada suhu percobaan adalah 0,465 N m-1. Kepadatan merkuri = 13,6 × 103 kg/m-3.
Jawab:
Sudut kontak antara merkuri dan soda lime glass, θ = 140 °
Radius dari tabung sempit, r = 1 mm = 1 × 10-3 m
tegangan permukaan air raksa pada suhu tertentu, s = 0,465 N m-1
Kepadatan merkuri, ρ = 13,6 × 103 kg / m3
Berenang di ketinggian raksa = h
Percepatan gravitasi, g = 9,8 m / s2
tegangan permukaan terkait dengan sudut kontak dan berenang di ketinggian seperti:
s = hρgr/2 cosθ
∴ h = 2s cosθ/ρgr
= 2 × 0,465 × cos1400 / (1 × 10-3 × 13,6 × 103 × 9,8)
= -0,00534 m
= -5,34 m
Di sini, tanda negatif menunjukkan tingkat penurunan raksa.
Radius dari tabung sempit, r = 1 mm = 1 × 10-3 m
tegangan permukaan air raksa pada suhu tertentu, s = 0,465 N m-1
Kepadatan merkuri, ρ = 13,6 × 103 kg / m3
Berenang di ketinggian raksa = h
Percepatan gravitasi, g = 9,8 m / s2
tegangan permukaan terkait dengan sudut kontak dan berenang di ketinggian seperti:
s = hρgr/2 cosθ
∴ h = 2s cosθ/ρgr
= 2 × 0,465 × cos1400 / (1 × 10-3 × 13,6 × 103 × 9,8)
= -0,00534 m
= -5,34 m
Di sini, tanda negatif menunjukkan tingkat penurunan raksa.
Soal 4: Dua pipa sempit diameter 3,0 mm dan 6,0 mm yang bergabung bersama untuk membentuk pipa-U terbuka di kedua ujungnya. Jika pipa-U berisi air, apa perbedaan ketinggian dalam dua kolom pipa? tegangan permukaan air pada suhu percobaan adalah 7.3 × 10-2 Nm-1. Ambil sudut kontak menjadi nol dan massa jenis air 1,0 × 103 kg m-3 (g = 9,8 m s-2).
Jawab:
Diameter pipa pertama, d1 = 3,0 mm = 3 × 10-3 m
Oleh karena itu, jari-jari pipa pertama, r1 = d1 / 2 = 1,5 × 10-3 m
Diameter pipa kedua, d2 = 6,0 mm = 6 × 10-3 mm
Oleh karena itu, jari-jari pipa kedua, r2 = d2 / 2 = 3 × 10-3m
tegangan permukaan air, s = 7,3 × 10-2 Nm-1
Sudut kontak antara permukaan pipa dan air, θ = 00
massa jenis air, ρ = 1,0 × 103 kg/m-3
Percepatan gravitasi, g = 9,8 m/s2
ketinggian air yang naik di tabung pertama dan kedua masing-masing adalah h1dan h2. ketinggian ini diberikan oleh hubungan:
h1 = 2s cosθ / r1ρg ..... (i)
h2 = 2s cosθ / r2ρg ..... (ii)
Perbedaan antara tingkat air di dua kaki dari tabung dapat dihitung sebagai:
Jawab:
Diameter pipa pertama, d1 = 3,0 mm = 3 × 10-3 m
Oleh karena itu, jari-jari pipa pertama, r1 = d1 / 2 = 1,5 × 10-3 m
Diameter pipa kedua, d2 = 6,0 mm = 6 × 10-3 mm
Oleh karena itu, jari-jari pipa kedua, r2 = d2 / 2 = 3 × 10-3m
tegangan permukaan air, s = 7,3 × 10-2 Nm-1
Sudut kontak antara permukaan pipa dan air, θ = 00
massa jenis air, ρ = 1,0 × 103 kg/m-3
Percepatan gravitasi, g = 9,8 m/s2
ketinggian air yang naik di tabung pertama dan kedua masing-masing adalah h1dan h2. ketinggian ini diberikan oleh hubungan:
h1 = 2s cosθ / r1ρg ..... (i)
h2 = 2s cosθ / r2ρg ..... (ii)
Perbedaan antara tingkat air di dua kaki dari tabung dapat dihitung sebagai:
= 4.966 × 10-3 m
= 4.97 mm
jadi perbedaan ketinggian air pada kedua pipa adalah 4,97 mm
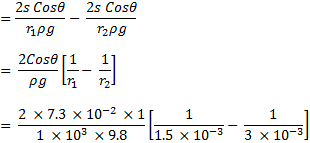
Tidak ada komentar:
Posting Komentar